Математика та архітектура

Математика та архітектура взаємопов'язані, оскільки як і в інших видах мистецтв, архітектори використовують математику для різних цілей. Крім математики для проектування будівель, архітектори використовують і геометрію: для визначення просторових форм; починаючи з піфагорійців, для створення форм, які вважаються гармонійними, та відповідно для планування будівель та їх оточення відповідно до математичних, естетичних і деколи релігійних принципів; для прикрашення будівель математичними об'єктами, наприклад теселяціями; та для досягнення «зелених» цілей, наприклад для мінімізації швидкості вітрів біля основ високих будівель.

«Огірок» (англ. The Gherkin), Сент-Мері Екс 30, Лондон, завершений 2003 року, — це параметрично проектоване тіло обертання.
Храм Кандарійя Махадев, Кхаджурахо, Індія, — приклад релігійної архітектури з фрактальною структурою, багато частини якої нагадують ціле. Бл. 1030 року[1]

У давньоєгипетській, давньогрецькій, індійській та ісламській архітектурах будівлі, включаючи піраміди, храми, мечеті, палаци та мавзолеї створювались з релігійних причин за певними пропорціями. В ісламській архітектурі], геометричні форми та стрічкові орнаменти використовувались для прикрашення будівель зовні та всередині. Деякі індуські храми структурою нагадують фрактали, де частина схожа на ціле, що передає ідею індуської космології. У XXI столітті математичні орнаменти знову використовуються для прикрашення публічних будівель.

В архітектурі Відродження, симетрія та пропорція навмисно підкреслювались такими світськими архітекторами як Леон-Баттіста Альберті, Себастьяно Серліо та Андреа Палладіо, що перебували під впливом давньоримського твору «De architectura» Вітрувія та давньогрецької арифметики піфагорейців.

Наприкінці XIX століття Володимир Шухов у Російській імперії та Антоніо Гауді у Барселоні стали піонерами використання гіперболоїдних конструкцій. У храмі Святого Сімейства Гауді також використав гіперболічні параболоїди, теселяції, ланцюгові арки, катеноїди, гелікоїди та лінійчаті поверхні.

У 20-му ст. такі стилі як модернізм та деконструктивізм досліджували різні геометрії для отримання бажаних ефектів. Так, мінімальні поверхні були використані у схожих на тент дахах Денверського міжнародного аеропорту, США, а Річард Бакмінстер Фуллер став піонером у використання сильних черепашкових структур відомих як геодезичний купол.

Пов'язані галузі
У часи Відродження, від архітектора як Леон-Баттіста Альберті очікували освіченість у багатьох дисциплінах, у тому числі в арифметиці та геометрії.

Архітектура та математика пов'язані принаймні з часів Античності. У Стародавньому Римі, Вітрувій визначав архітектора як людину, яка знала ряд інших дисциплін, в першу чергу геометрію, що дозволяло йому наглядати за майстрами у всіх інших галузях будівництва, наприклад за каменярами та столярами. Те саме вимагалось в і Середньовіччі, коли студенти-архітектори вивчали арифметику, геометрію та естетику поруч зі стандартними граматикою, логікою та риторикою (тривіум), а майстер-будівельник на піку кар'єри отримував титул архітектора чи інженера. У часи Відродження, цей додатковий план навчання став квадривіумом арифметики, геометрії, музики та астрономії, — науки, знання яких очікувалось від людини епохи Відродження як Леон-Баттіста Альберті. Відомий і сьогодні англійський архітектор сер Крістофер Рен, у свій час був в першу чергу відомий як астроном[2].

Вільямс та Оствальд у дослідженні взаємодії математики та архітектури починаючи з 1500 року з використанням підходу німецького соціолога Теодора Адорно визначають три тенденції серед архітекторів, а саме: бути революціонером, пропонуючи повністю нові ідеї; бути реакціонером, не пропонуючи змін; або пропагувати відродження, тобто рухатись назад. Вони доводять, що у часи реакції чи відродження архітектори уникали звернення до математика за натхненням. Це могло б пояснити, чому у періоди відродження, наприклад у неоготиці Англії XIX століття, архітектура практично не мала зв'язку з математикою. Аналогічно у часи реакції, які як італійський маньєризм 1520—1580 років, чи бароко та палладіанство XVII століття, до математики майже не звертались. Натомість, революційні рухи початку 20-го ст., такі як футуризм та конструктивізм активно відкидали старі ідеї та використовуючи математику, призвели до архітектури модернізму. Наприкінці XX століття фракталльна геометрія та аперіодичний поділ площини були швидко сприйняті архітекторами та використані у створенні зовнішнього оздоблення споруд[3].

Крім власне необхідності математики для проектування (обрахунку) будівель, архітектори використовують її і для інших цілей[4]:

  • по-перше, вони використовують геометрію, яка визначає просторові форми[5];
  • по-друге, вони використовують математику для проектування форм, які вважаються красивими або гармонійними[6]. З часів піфагорійців з їх релігійною філософією числа[7], архітектори Стародавньої Греції, Стародавнього Риму, ісламського світу та італійського Відродження обирали пропорції будівель та їх оточення у відповідності до математичних, естетичних та деколи релігійних принципів[8][9][10][11];
  • по-третє, вони можуть використовувати математичні об'єкти, такі як теселяції для оздоблення будівель[12][13];
  • в четверте, вони можуть використовувати математику за допомогою комп'ютерних моделей для вирішення екологічних питань, наприклад мінімізації закручення потоків вітру внизу хмарочосів[14].

Гармонійні просторові форми

Стародавній Рим
План грецького будинку за Вітрувієм
Вітрувій
Інтер'єр Пантеону, картина роботи Джованні Паоло Паніні, 1758

Впливовий давньоримський архітектор Вітрувій доводив, що дизайн будівлі такої як храм залежить від двох характеристик — симетрії та пропорції. Пропорція забезпечує, щоб кожна частина будівлі гармонійно пов'язувалася зі всіма іншими частинами. Симетрія у розумінні Вітрувія за змістом відповідала більше поняттю «модульна структура», а не «осьова симетрія», оскільки вона також стосувалася поєднанню (модульних) частин будівлі у ціле. У його базиліці у Фано, Вітрувій використав співвідношення малих цілих чисел, особливо трикутних чисел (1, 3, 6, 10, …) для створення пропорційного поділу будівлі на (вітрувіанські) модулі.[lower-alpha 1] Тому, співвідношення ширини до довжини базиліки становить 1:2; неф довкола неї має однакову ширину та висоту, 1:1; колони мають товщину 5 футів та висоту 50 футів, 1:10.[8]

Поземний план Пантеона

У трактаті «De architectura» (бл. 15 р. до н. е.) Вітрувій назвав три якості, які вимагаються від архітектури будівлі: стійкість, корисність та насолода. Ця якості модна використати як категорії для класифікації використання математики у архітектурі. Стійкість охоплює використання математики для забезпечення стійкості будівлі, її стабільності та запланованої поведінки .(наприклад при землетрусах). Корисність частково походить з ефективного використання математики для створення та аналізу просторових та інших відносин у проектуванні. Насолода — це атрибут збудованої споруди, що походиить від втілення математичних відносин у будівлі і включає естетичні, чуттєві та інтелектуальні якості[16].

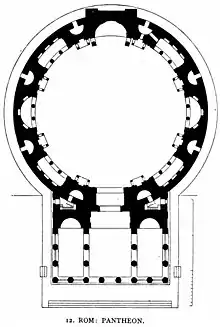
Пантеон

Римський Пантеон вцілів неушкодженим та демонструє класичну римську структуру, пропорцію та оздоблення. Основна його конструкція — купол, вершина якого має круглий отвір для потрапляння світла; попереду куполу розташована коротка колонада з трикутним фронтоном. Висота до отвору та діаметр внутрішнього кола однакові — 43,3 метри, тому весь інтер'єр точно впишеться у куб, а в нього можна вписати сферу такого самого діаметра[17]. Ці значення легше сприймати, якщо представити їх у давньоримських одиницях вимірювання: діаметр куполу становить 150 римських футів,; отвір згори має діаметр 30 римських футів, а двері — 40 римських футів у висоту[18]. Пантеон залишається найбільшим в світі неармованим бетонним куполом[19].

Відродження
Фасад церкви Санта Марія Новелла, Флоренція, 1470. Фріз (з квадратами) та вище — робота Леона-Баттіста Альберті.

Леон-Баттіста Альберті написав перший трактат часів Відродження про архітектуру — «De re aedificatoria» (Про мистецтво будівництва), який став і першою надрукованою книгою про архітектуру 1485 року. Вона частково спирається на «De architectura» Вітрувія, та, через Нікомаха, на піфагорейську арифметику. Альберті починає з куба та виводить з нього співвідношення: діагональ сторони дає співвідношення 1:√2, а діаметр сфери, в які вписаний куб — співвідношення 1:√3.[20][21] Альберті також задокументував відкриття Філіппо Брунеллескі лінійної перспективи, розробленої для проектування будівель, які будуть виглядати красиво пропорційними при спогляданні з певної відстані[11].

Архітектурна перспектива декорації сцени роботи Себастьяно Серліо, 1569[22]

Другим важливим трактатом став «Regole generali d'architettura» (Загальні правила архітектури) Себастьяно Серліо, перший том яких з'явився у Венеції 1537; том 1545 року (книги 1 та 2) розповідав про геометрію та перспективу. Два методи Серліо з конструювання перспективи були неправильні, але це не завадило широкому використанню книги[23].

План та розріз Вілли Пізані роботи Андреа Палладіо

У 1570 році у Венеції Андреа Палладіо надрукував впливову працю «Чотири книги про архітектуру». Поширений друк цієї книги значною мірою сприяв поширенню ідей італійського Відродження на Європу, за допомогою таких прихильників як англійський дипломат Генрі Воттон з його книгою 1624 року «елементи архітектури»[24]. Палладіо розраховував пропорції кожної кімнати у віллі за допомогою простих математичних співвідношень, наприклад 3:4 та 4:5, і різні кімнати в будинку були пов'язані з цими співвідношеннями. Попередні архітектори використовували ці формули для балансування єдиного симетричного фасаду, а проекти Палладіо використовували їх у всій, як правило квадратній, віллі[25] Палладіо у «Quattro libri» дозволив деякі співвідношення, зазначивши[26]:

Існує сім типів приміщень, які найбільш красиві, добре виважені та гарно виходять: круглі, хоча це рідко; або квадратні; або їх довжина дорівнює діагоналі квадрату ширини; або квадрат та третина; або квадрат і половина; або квадрат і дві третини; або два квадрати.[27][lower-alpha 2]

Вінченцо Скамоцці 1615 року надрукував трактат пізнього Відродження «L'Idea dell'Architettura Universale» (Ідея універсальної архітектури)[28], в якому намагався пов'язати дизайн міст та будівель з ідеями Вітрувія і піфагорейців та більш сучасними йому ідеями Палладіо[29].

XIX століття
Гіперболоїдне мереживо Аджигольського маяка Володимира Шухова, Україна, 1911

Володимир Шухов наприкінці XIX століття почав використовувати гіперболоїдні конструкції для опор, маяків та градирень. Їх яскрава форма одночасно естетично цікава та міцна, і економно використовує будівельні матеріали. Перша Шуховська вежа демонструвалась у Нижньому Новгороді 1896 року.[30][31][32]

XX століття
Площини стилю De Stijl, що ковзають та перехрещуються: Будинок Шредер, 1924

Мистецький рух початку 20-го ст. — модерністська архітектура, використовував прямокутну евклідову геометрію. На думку руху De Stijl горизонталі та вертикалі були частиною універсального, а архітектурна форма є складанням разом цих двох напрямків, використовуючи площини дахів, стін, балконів, які або «ковзають» один по одному або перетинаються, наприклад як у будинку Шредер 1924 року за проектом Герріта Рітвельда.[33]

Мак та сільничка (біометрика) Рауля Генріха Франса, зображення з «Die Pflanze als Erfinder» (Рослини як винахідник), 1920

Модерністські архітектори вільно використовували не лише площини, а й кривини. Так станція лондонського метро «Арнос Гроув» 1933 року роботи Чарльза Холдена має круглий цегляний вестибюль з пласким бетонним дахом.[34] У 1938 році, художник напрямку Баухаус Лазло Мохолі-Наг взяв у використання сім біотехнічних елементів Рауля Генріха Франса, а саме кристал, сферу, конус, площину, (кубоїдну) стрічку, (циліндричний) стрижень та спіраль, як базові будівельні блоки архітектури, натхненної природою.[35][36]

Ле Корбюзьє запропонував антропометричну шкалу пропорцій в архітектурі «модулор», яка була заснована на припущення про зріст чоловіка[37]. Його каплиця Нотр-Дам-дю-О 1955 року використовує вільні криві, які не можна описати математичними формулами[lower-alpha 3] Вважається, що її форми наслідують природні, наприклад ніс корабля або руки, складені у молитві[40]. Проект присутній лише на найбільшому масштабі: ієрархія деталей на менших масштабах відсутня, а тому відсутній фрактальний вимір; те саме стосується і інших відомих будівель XX століття — Сіднейського оперного театру, Міжнародного аеропорту Денвера та музею Гуггенгайма в Більбао[38].

Сучасна архітектура, на думку самих ведучих архітекторів, висловлену в опитуванні 2010 року «World Architecture Survey», є надзвичайно різноманітною; найкращим прикладом вони визначили музей Гуггенгайма у Більбао роботи Франка Гері.[41]

Мінімальні поверхні тканинного даху Денверського міжнародного аеропорту

Будівля терміналу Денверського міжнародного аеропорту, завершена 1995 року, має тканинний дах, що підтримується сталевими тросами, який є мінімальною поверхнею] (тобто її середня кривина — нуль), що нагадує покриті снігом вершини Колорадо та тенти тіпі корінних народів США.[42][43]

Архітектор Річард Бакмінстер Фуллер знаменитий проектуванням сильних тонких конструкцій відомих як геодезичний купол. Купол монреальської Біосфери має 61 м у висоту та діаметр 76 м.[44]

Сіднейський оперний театр має вражаючий вітрилоподібний дах, який складається з білих арок; для їх створення з стандартизованих частин були розроблені трикутні секції сферичних оболонок однакового радіусу. Вони всі мають необхідну однакову кривину у всіх напрямках[45].

Мистецький рух кінця XX століття «Деконструктивізм» створює продуманий безлад за рахунок «випадкових форм»[46] of high complexity[47], використовуючи непаралельні стіни, решітки, що накладаються одна на одну, та складні двовимірні поверхні, наприклад у роботах Френка Гері Концертна зала Диснея та Музей Гугенхайма в Більбао[48][49].

До двадцятого сторіччя студенти-архітектори повинні були мати знання з математики. Нікос Салінгарос доводить, що спочатку «надмірно спрощений та заполітизований» модернізм, а потім "анти-науковий деконструктивізм фактично відділили архітектуру від математики, виховавши архітекторів, які «відкидають математичну інформацію у будівництві, і це шкодить суспільству».[38]

  • Нова об'єктивність: баухаус Вальтера Гропіуса, Дессау, 1925
  • Циліндр: станція метро «Арнос Гроув» Чарльза Холдена, 1933
  • Гіодезійний купол: монреальська Біосфера, 1967
  • Однакова кривина: Сіднейський оперний театр, 1973
  • Деконструктивізм: Концертна зала Діснея, 2003

Стародавній Єгипет
Піраміди в Гізі, свідомо чи випадково, мають математичні пропорції.
У пірамідах типу піраміди Хеопса співвідношення «основа: гіпотенуза» (b: a) може бутии: 1:φ (трикутник Кеплера), 3:5 (трикутник 3-4-5) або 1:4/π

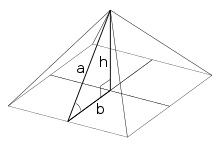
Піраміди Стародавнього Єгипту — це мавзолеї, збудовані за спеціально обраними пропорціями, але триває суперечка за якими саме. Співвідношення похилої висоти до половини довжини основи становить 1,619, що лише на 1 % відрізняється від золотого перетину. Якщо так було задумано, це вказує на використання трикутника Кеплера (передній кут 51°49’)[50][51]. Однак, з більшою ймовірністю піраміди будувалися за трикутником 3-4-5 (передній кут 53°8’), який був відомий єгиптянам, про що свідчить Папірус Рінда (бл. 1650—1550 р. до н. е.), або за трикутником, співвідношення основи до гіпотенузи 1:4/π (передній кут 51°50’)[52].

Стародавня Індія
Світова пам'ятка ЮНЕСКО — індуський храм Вірупакша у Хампі має схожу на фрактала конструкцію, де частини нагадують ціле.

Васту-шастра, стародавні індійські канони архітектури та містопланування, використовують симетричні креслення — мандали. Для отримання вимірів будівлі та її компонентів використовувались складні розрахунки. Проекти намагались пристосувати архітектуру до природи, відповідних функцій окремих частин споруди на стародавніх вірувань за допомогою геометричних орнаментів, (янтр), симетрії та розташування за сторонами світу[53][54]. Однак давні будівельними могли натрапити на математичні пропорції випадково — Джордж Іфра зазначає, що прості «фокуси» з мотузкою та кілками можуть бути використані для розмітки геометричних форм, таких як еліпси та прямі кути[11][55].

План храму Мінакші, Мадурай, який будувався з 7 ст. н. е. Четверо воріт (номери I—IV) — це високі гопурами.

Математика фракталів використовувалась для демонстрації причин, чому наявні будівлі мають універсальну привабливість та візуально приємні, а саме тому, що вони надають глядачу відчуття масштабу при спогляданні на різних відстанях. Наприклад, в таких індуських храмах як Вірупакша у Хампі (з 7 ст. н. е.) та Кандарійя Махадев у Кхаджурахо, частина та ціле мають однаковий вигляд, з фрактальною розмірністю від 1,7 до 1,8. Накопичення маленьких веж (шикхара, букв. 'гор') довкола найбільшої центральної вежі, яка є символом святої гори Кайлас, домівки Шиви, зображує нескінченне повторення всесвітів в індуській космології[1][56]. Таке групування менших веж довкола більших повторюється на менших масштабах.

Храм Мінакші — великий комплекс з численними святилищами, а вулиці міста Мадурай спроектовані концентрично довкола храму у відповідності до шастр. Чотири входи — високі вежі (гопурами) зі схожою на фрактали структурою, як в і Хампі. Дворики навколо кожного святилищі — прямокутні та оточені високими стінами[57].

Стародавня Греція
Парфенон was designed using Pythagorean ratios.

Піфагор (бл. 569 — бл. 475 рр.до н. е.) та його послідовники — піфагорійці, вважали, що «все є числами». Вони досліджували гармонії, створені нотами з конкретними співвідношеннями частоти на основі малих цілих чисел та стверджували, що і будівлі слід проектувати за такими співвідношеннями. Грецьке слово «симетрія» початково означало гармонію архітектурних форм, виконану у чітких співвідношеннях від найменшої деталі до всього проєкту будинку[11].

Поземний план Парфенона

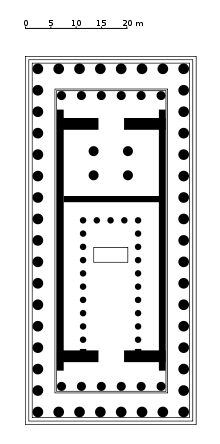
Парфенон має довжину 69,5 метрів, ширину — 30,9 метрів та висоту до карнизу — 13,7 метрів, що відповідає співвідношенню 4:9 як для ширини і довжини, так і для висоти та ширини. Співвідношення висота: ширина: довжина становить 16:36:81, або 42:62:92. Чотирикутник зі сторонами 4:9 може були збудованих з трьох чотирикутників зі сторонами 3:4, а кожна половина таких чотирикутників (по діагоналі) дає прямокутний трикутник зі сторонами 3:4:5, що дозволяє перевірку сторін та кутів за допомогою простої мотузки з вузлами на відповідних відстанях. Внутрішній простір (наос) Парфенону так само має пропорції 4:9 (21,44 м у ширину та 48,3 м у довжину); співвідношення між діаметром зовнішніх колон (1,905м) та відстанню між їх центрами (4,293 м) також становить 4:9.[11]

Парфенон вважається «ідеальним доричним храмом, коли-небудь збудованим».[58] Його архітектурні тонкощі включають «тонку відповідність між вигином стилобату, кривиною стін наосу та ентазисом колон».[58] Ентазис — це незначне витончення колон у діаметрі по мірі зростання їх висоти. Як і в інших грецьких храмах[59], стилобат, платформа, на якій стоять колони, маж невеликий параболічний вигин з метою стоку дощової води та кращої стійкості при землетрусах. Тому колони мали б мати невеликий ухил назовні, але насправді вони мають невеликий ухил всередину (якщо уявно продовжити колони вгору, вони зустрінуться десь у 1,6 км над центром будівлі. Оскільки всі колони мають однакову висоту, вигин зовнішнього краю стилобату передається архітраву та даху над ним: «всі слідують правилу побудови з незначним вигином».[60]

Золотий перетин вже був відомий 300 р. до н. е., коли Евклід описав метод геометричної побудови[61]. Існують теорії, що він був використаний у проектуванні Парфенону та інших давньогрецьких будівлях, а також в скульптурах, картинах та кераміці[62]. Інші автори однак піддають все це сумніву[63]. Наприклад експерименти Джорджа Марковскі не виявили жодної переваги золотому чотирикутнику[64].

Ісламська архітектура
Левовий двір в Альгамбрі має жорсткі пропорції, засновані на квадратних коренях малих цілих чисел.

Антоніо Фернандес-Пуертас припускає, що і Альгамбра, і Мескіта[65], були проектовані з використанням іспано-мусульманського футу або кодо довжиною бл. 62 см. У Левовому дворі Альгамбри пропорції відповідають серії квадратних коренів малих цілих чисел. Прямокутник зі сторонами 1 та √2 має (за теоремою Піфагора) діагональ √3, що відповідає прямокутному трикутнику зі сторін Левового двору; серія продовжується √4 (що дає співвідношення 1:2), √5 і т. д. Декоративні орнаменти мають схожі пропорції, де √2 утворює кола у квадратах та восьмикутні зірки, а √3 — шестикутні зірки. Однак відсутні докази раніше висловленого припущення, що в Альгамбрі використовувався «золотий перетин»[9][66]. По боках Левового двору розташовані Двір двох сестер та Двір Абенчерайєс (ісп. Abencerrajes); можна намалювати правильний шестикутник, використавши як вершини центри цих двох дворів та чотири внутрішні кути Левового двору[67].

Мечеть Селіміє, 1569—1575

Мечеть Селіміє в Едірне, Туреччина, була збудована Сінаном так, що міхраб можна побачити з будь-якої точки всередині будівлі. Дуже великий центральний простір має форму восьмикутника, вершинами якого є 8 величезних колон, та накритий круглим куполом діаметром 31,25 м та висотою 43 м. Восьмикутник переходить у квадрат за рахунок чотирьох напівкуполів, які зовні увінчані чотирма мінаретами 83 м у висоту. Таким чином поземний план будівлі виглядає як коло, вписане у восьмикутник, вписаний у квадрат[68].

Могольська архітектура
Комплекс Тадж Махал в Агрі

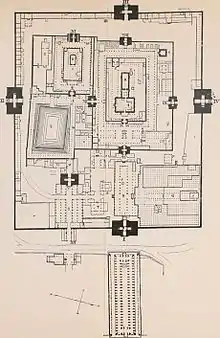
Могольська архітектура, як видно наприклад у покинутій імперській столиці Фатехпур-Сікрі та у комплексі Тадж Махал, мала чіткий математичний порядок та сильну естетику на основі симетрії та гармонії[10][69].

Тадж Махал є є ідеальним прикладом могольської архітектури, одночасно зображуючи рай і владу могольського володаря Шаха Джахана своїм масштабом, симетрією та дорогим оздобленням. Білий мармур мавзолею, прикрашений п'єтра дура італ. pietra dura, інкрустацією з каміння), великі ворота Дарваза-і-Рауза, інші будівлі, сади та доріжки разом складають єдиний ієрархічний дизайн. До інших будівель належать мечеть з червоного пісковика на захід та майже ідентична будівля — Джаваб або «відповідь» зі сходу для підтримки двосторонньої симетрії комплексу. Формальний сад чахар-бак складається з 4-х частин, які символізують чотири ріки раю та пропонують види та відзеркалення мавзолею. Сади поділені на 16 партерів[70].

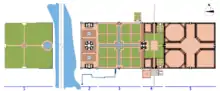
План комплексу Тадж Махал. Великі ворота справа, мавзолей по центру біля ріки, по боках мечеть (знизу) та джаваб (згори). На плані видно квадрати та восьмикутники.

Комплекс Тадж Махал був спланований на решітці, поділений на менші решітки. За аналізом решіток 2006 року Кох та Барро погодились з традиційними оповідями про ширину комплексу у 374 зіри,[lower-alpha 4] та площу основної частини у три квадрати зі стороною 374 зіри. Ці квадрати були поділені на ділянки різного призначення, наприклад базар та караван-сарай, модулями по 17 зір; сад та тераси поділені модулями по 23 зіри та мають загальну ширину 368 зір (16 x 23). Мавзолей, мечеть та джаваб розташовані на решітці з модулями по 7 зір. Кох та Барро зазначають, що якщо восьмикутника, який постійно використовується у комплексі, встановити ширину у 7 одиниць, його ширина складе 17 одиниць[lower-alpha 5], що може допомогти у поясненні співвідношень комплексу[71].

Християнська архітектура
Хагія Софія, Стамбул
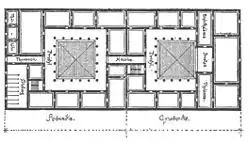
a) План галереї (верх)
b) План першого поверху (низ)

Християнська патріархальна базиліка Хагія Софія у Візантіумі (тепер Стамбул), вперше збудована 537 року (та двічі перебудована), тисячу років [lower-alpha 6] була найбільшим собором. Вона надихнула багато будівель, у тому числі Блакитну та інші мечеті в самому місті. Архітектура Візантійської імперії у базиліці включає наву, увінчану круглим куполом та двома напівкуполами, всі одного діаметра (31 метр), а ще 5 менших напівкуполів формують апсиду та чотири закруглені кути величезного прямокутного інтер'єру[72]. Середньовічні архітектори інтерпретували це як повсякденну землю (квадратна основа) та божественні небеса (сферичний купол згори)[73]. Імператор Юстиніан I залучив двох геометрів, Ісидора Мілетського та Анфемія Траллського, як архітекторів собору. Ісидор збирав праці Архімеда про геометрію тіл, та перебував під його впливом[11][74].

Важливість у християнстві водяного хрещення знайшла відображення у масштабах архітектури баптистеріїв. Найстаріший з тих, що збереглися, — Латеранський баптистерій у Римі, збудований 440 року,[75] задав тенденцію до восьмикутних баптистеріїв; хрестильна купіль в таких будівлях також часто була восьмикутною. Хоча найбільший в Італії Пізанський баптистерій, збудований між 1152 та 1363 роками, за формою круглий, з восьмикутною купіллю. Він має 54,86 м у висоту та діаметр 34,13 м (співвідношення 8:5).[76] Святий Амвросій писав, що купелі та баптистерії були восьмикутні, оскільки «на восьмий день[lower-alpha 7] воскресінням, Христос послаблює пута смерті і отримує мертвих з могил.»[77][78] Святий Августин аналогічно описав восьмий день як «вічний … освячений воскресінням Христа».[78][79].

Восьмикутний баптистерій Святого Івана у Флоренції, збудований між 1059 та 1128 роками, є однією з найстаріших будівель у місті та однією з останніх, збудований у прямій традиції класичної античності; він був дуже впливовим у часи флорентійського Відродження, оскільки основні архітектори, у тому числі Франческо Таленті, Альберті та Брунеллескі використовували його як зразок класичної архітектури[80].

У Чехії число п'ять було «рясно»[81] використано у церкві святого Яна Непомуцького 1721 року у Зеленій горі, поблизу Ждяр-над-Сазавою, спроектованій Яном Блажеєм Сантіні Айхлом. Нава є круглою, оточеною п'ятьма парами колон та п'ятьма овальними куполами, які чергуються зі стрілчастими арками. Церква має 5 входів, 5 каплиць, 5 вівтарів та 5 зірок; легенда стверджує, що коли Ян Непомуцький був замучений, над його головою з'явилися 5 зірок[81][82]. П'ятикратна архітектура також може символізувати 5 ран Христа та 5 літер «Tacui» (з латини: «я мовчу» [про таємницю сповіді])[83].

У Саграда Фамілія, Барселона, будівництво якого розпочато 1882 році (і не завершено на 2015 рік), Антоніо Гауді використав різноманітні геометричні структури, деякі з яких є мінімальними поверхнями, у тому числі гіперболічні параболоїди та гіперболоїдні тіла обертання[84], теселяції, ланцюгові арки, катеноїди, гелікоїди та лінійчаті поверхні. Ця суміш геометрів креативно поєднана різним чином по всій церкві. Наприклад, на фасаді Страстей Господніх Гауді зібрав кам'яні «гілки» у формі гіперболічних параболоїдів, які перетинаються на своїх вершинах (директрисах) і відповідно не сходяться в точку. На противагу цьому, у колонаді гіперболічні параболоїдні поверхні плавно поєднуються з іншими структурами та формують безперервні поверхні. Крім того, Гауді використовує природні патерни, самі по собі математичні: колони за формою дерев та віконні перемички, створені з необробленого базальту, розколотого природним чином (при охолодженні розплавленого каменю) на шестикутні колони[85][86][87].

Собор Успіння Діви Марії 1971 року у Сан-Франциско, США, має дах у формі сідла, створений з 8 сегментів гіперболічних параболоїдів, розташованих таким чином, що горизонтальний перетин даху має форму квадрату, а верхній перетин — форму хреста. Сама будівля квадратна зі стороною 77,7 метрів та висотою 57,9 метрів[88].

Бразильський собор 1970 року за проектом Оскара Німеєра по іншому використовує гіперболоїдну структуру; він збудований з 16 однакових бетонних балок, кожна вагою 90 тонн, поставлених по колу, — вони утворюють гіперболоїдне тіло обертання, та здаються стилізованими руками, які моляться небесам. Зовні видно лише купол, більшість будівлі розташована під землею[89][90][91][92].

  • Склепіння нави Хагія Софія, Стамбул, 562
  • Восьмикутний баптистерій Св.Івана, Флоренція, 1128
  • 5-кратна симетрія: церква Св.Яна Непомуцького, 1721
  • Фасад Притрастей Саграда Фамілія, Барселона, розп.1882
  • Бразильський собор, 1970
  • Собор Успіння Діви Марії, Сан-Франциско, 1971

Математичне оздоблення

Ісламське архітектурне оздоблення
The complex geometry and tilings of the muqarnas vaulting in the Sheikh Lotfollah Mosque, Ісфахан, 1603—1619

Ісламські будівлі часто оздоблені геометричними орнаментами, які як правило використовують декілька математичних теселяцій, виконаних з керамічної плитки (джиріх, зулляйдж), яка може бути однотонною або прикрашеною стрічками[11]. В таких орнаментах використовуються симетрії, наприклад зірки з 6 чи 8 кутами та багатогранники. Деякі з них засновані на «Хатем Сулемані» або мотиві печатки Соломона, яка була у форми восьмикутної зірки, утвореної двома квадратами, один з яких повернутий на 45° відносно спільного центру[93]. В ісламських орнаментах використовується більшість з 17 можливих груп шпалер; ще 1944 року Едіт Мюллер показала, що в оздобленні Альгамбри використані 11 груп шпалер, а 1986 Бранко Ґрюнбаум стверджував, що знайшов там 13 груп, та породив контроверзу, що інші 4 групи не присутні ніде в ісламському орнаменті[93].

Сучасне архітектурне оздоблення

Наприкінці 20-го сторіччя новітні математичні утворення, такі як фрактальна геометрія та аперіодичний поділ, почали використовуватись архітекторами для утворення цікавих та привабливих оздоблень для будівель[3]. 1913 року модерністський архітектор Адольф Лоос заявив, що "орнамент — це злочин[94], що вплинуло на архітектурну думку всього 20-го сторіччя. У XXI столітті архітектори знову починають досліджувати використання орнаменту, і його використання надзвичайно різноманітне. Так наприклад Концертний та конференц-центр «Харпа», збудований 2011 року за проектом Геннінга Ларсена у Рейк'явіку, має схожу на кришталеву скелю стіну з великих блоків скла[94]. Ревенсборнський коледж, створений 2010 року за проектом «Foreign Office Architects» у Лондоні, декоративно тесельований 28 000 плитками з анодованого алюмінію червоного, білого та коричневого кольору, які поєднують круглі вікна різних розмірів. Теселяція використовує три типи плитки — рівносторонній трикутник та два неправильні п'ятикутники[95][96][lower-alpha 8] Бібліотека Каназава Умімірай за проектом Казумі Кудо має декоративну решітку, створену з малих циліндричних блоків, вмурованих у неоздоблені бетонні стіни.[94]

  • Ревенсборнський коледж, 2010
  • Бібліотека Каназава Умімірай, 2011

Захист

У періоді між серединою XV та XIX століттям архітектура фортифікацій розвивалась від середньовічних фортець, які мали високі кам'яні стіни, до низьких симетричних фортець-зірок, які були здатні протистояти артилерії. Геометрія форми зірки була викликана необхідністю уникнути мертвих зон, в яких атакуюча піхота може сховатись від вогню захисників; стороні кутів зіркі були виконані під таким кутом, щоб дозволити перехресних вогонь з вершин кутів, який би продовжувався і далі за ними. Таку фортеці проектували відомі архітектори, серед них Мікеланджело Буонарроті, Бальдазаре Перуцці, Вінченцо Скамоцці та Себаст'єн ле Претр де Вобан[97][98].

Історик архітектури Зігфрід Гідіон доводив, що фортеці-зірки мали вирішальний вплив на структурування ідеального міста Відродження: «Відродження було загіпнотизовано одним типом міста, які протягом півтора століття — від Філарете до Скамоцці — насаджувалось на всі утопічні схеми, — це місто у формі зірки»[99].

  • Фортифікаційний план Коевордена (XVII століття)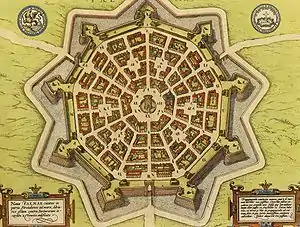
  • Палманова, венеційське місто, Італія, в межах фортеці-зірки (XVII століття)

Захист навколишнього середовища
Якчал у Язді, Іран

Архітектори можуть обирати форму будівлі для досягнення певних цілей з захисту навколишнього середовища[81]. Наприклад, хмарочос Сент-Мері Екс 30, Лондон, архітекторів Foster and Partners, відомий як «Огірок» за його форму, схожу на огірок, — це тіло обертання, спроектоване з використанням параметричного моделювання. Його геометрія була обрана не лише з чисто естетичних причин, а й для мінімізації вихорів повітря по його низу. Незважаючи на те, що його поверхня є викривленою, всі скляні панелі поверхні є пласкими, крім лінзи нагорі. Більшість з панелей є чотирикутниками, оскільки вони всі можуть бути вирізані з прямокутного скла з меншими втратами ніж трикутні панелі[14].

Традиційні якчали (крижані ями) Персії функціонували як холодильники за методом випаровування. Над землею, споруда мала форму купола, а нижче рівня землі мала помешкання для криги та деколи і для їжі. Підземний простір та товсті стіни, які зберігали прохолоду, ізолювали простір всередині увесь рік. Внутрішній простір часто додатково охолоджуався за допомогою бадгірів. Це дозволяло влітку мати кригу, заготовлену взимку, для виготовлення з неї заморожених десертів[100].

Див. також

Нотатки
  1. У книзі 4, главі 3 трактату «De architectura», він прямо обговорює ці модулі[15]
  2. Сучасним алгебраїчним записом це відповідно 1:1, √2:1, 4:3, 3:2, 5:3, 2:1.
  3. Деякі дослідники, наприклад Нікос Салінгарос, заперечують це[38], однак не точно зрозуміло, які математичні формули виражені кривими каплиці Корбюзьє[39]
  4. 1 зіра - бл. 86 см.
  6. до завершення Севільського собору 1520 року
  7. Шостим днем Страсного тижня була Страсна п'ятниця; наступна неділя (день воскресіння) відповідно була восьмим днем.[77]
  8. Розглядався аперіодичний поділ для уникнення ритму структурної решітки, але на практиці мозаїка Пенроуза виявилась дуже складною, тому була обрана решітка 2,625 м горизонтально та 4,55 вертикально[96]

Примітки
  1. Rian, Iasef Md; Park, Jin-Ho; Ahn, Hyung Uk; Chang, Dongkuk (2007). Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho. Building and Environment 42. с. 4093–4107. doi:10.1016/j.buildenv.2007.01.028.
  2. Williams, Kim; Ostwald, Michael J., ред. (2015). Architecture and Mathematics from Antiquity to the Future: Volume I: from Antiquity to the 1500s. Birkhäuser. с. chapter 1. 1–24. ISBN 978-3-319-00136-4.
  3. Williams, Kim; Ostwald, Michael J., ред. (2015). Architecture and Mathematics from Antiquity to the Future: Volume II: The 1500s to the Future. Birkhäuser. с. chapter 48. 1–24. ISBN 978-3-319-00142-5.
  4. Architectural Engineering Overview. Sloan Career Cornerstone Center. Архів оригіналу за 14 липня 2015. Процитовано 11 жовтня 2015.
  5. Leyton, Michael (2001). A Generative Theory of Shape. Springer. ISBN 978-3-540-42717-9.
  6. Stakhov, Alexey; Olsen, Olsen (2009). The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science. World Scientific. ISBN 978-981-277-582-5.
  7. Smith, William (1870). Dictionary of Greek and Roman Biography and Mythology. Little, Brown. с. 620.
  8. Vitruvius (2009). On Architecture. Penguin Books. с. 8–9. ISBN 978-0-14-193195-1.
  9. Tennant, Raymond (July 2003). International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES, Mathematical Connections in Art Music, and Science, University of Granada, Spain, July, 2003 459 Islamic Constructions: The Geometry Needed by Craftsmen. International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES, Mathematical Connections in Art Music, and Science.
  10. Rai, Jaswant (1993). Mathematics and Aesthetics in Islamic Architecture: Reference to Fatehpur Sikri. Journal of King Saud University, Architecture & Planning 5 (1). с. 19–48.[недоступне посилання з квітня 2019]
  11. O'Connor, J. J.; Robertson, E. F. (February 2002). Mathematics and Architecture. University of St Andrews. Процитовано 4 жовтня 2015.
  12. van den Hoeven, Saskia; van der Veen, Maartje (2010). Muqarnas: Mathematics in Islamic Arts. Utrecht University. Архів оригіналу за 4 березня 2016. Процитовано 30 вересня 2015.
  13. Cucker, Felix (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. с. 103–106. ISBN 978-0-521-72876-8.
  14. Freiberger, Marianne (1 березня 2007). Perfect buildings: the maths of modern architecture. Plus magazine. Процитовано 5 жовтня 2015.
  15. Vitruvius. VITRUVIUS, BOOK IV, CHAPTER 3 On the Doric order. Vitruvius.be. Процитовано 6 жовтня 2015.
  16. Williams, Kim; Ostwald, Michael J. (9 лютого 2015). Architecture and Mathematics from Antiquity to the Future: Volume I: Antiquity to the 1500s. Birkhäuser. с. 42, 48. ISBN 978-3-319-00137-1.
  17. Roth, Leland M. (1992). Understanding Architecture: Its Elements, History, And Meaning. Boulder: Westview Press. с. 36. ISBN 0-06-438493-4.
  18. Claridge, Amanda (1998). Rome. Oxford Archaeological Guides. Oxford Oxfordshire: Oxford University Press. с. 204–5. ISBN 0-19-288003-9.
  19. Lancaster, Lynne C. (2005). Concrete Vaulted Construction in Imperial Rome: Innovations in Context. Cambridge: Cambridge University Press. с. 44–46. ISBN 0-521-84202-6.
  20. March, Lionel (1996). Renaissance mathematics and architectural proportion in Alberti's De re aedificatoria. Architectural Research Quarterly 2 (1). с. 54–65. doi:10.1017/S135913550000110X.
  21. Sphere circumscribing a cube. Mathalino.com Engineering Math Review. Процитовано 4 жовтня 2015.
  22. Typ 525.69.781, Houghton Library, Harvard University
  23. Andersen, Kirsti (2008). The Geometry of an Art: The History of the Mathematical Theory of Perspective from Alberti to Monge. Springer. с. 117–121. ISBN 978-0-387-48946-9.
  24. Ruhl, Carsten (7 квітня 2011). Palladianism: From the Italian Villa to International Architecture. European History Online. Процитовано 3 жовтня 2015.
  25. Copplestone, Trewin (1963). World Architecture. Hamlyn. с. 251.
  26. Wassell, Stephen R. The Mathematics Of Palladio's Villas: Workshop '98. Nexus Network Journal. Процитовано 3 жовтня 2015.
  27. Palladio, Andrea; Tavernor, Robert; Schofield, Richard (trans.) (1997) [1570]. I quattro libri dell'architettura. MIT Press. с. book I, chapter xxi, page 57.
  28. Scamozzi, Vincenzo; Vroom, W. H. M. (trans.) (2003) [1615]. The Idea of a Universal Architecture. Architectura & Natura.
  29. Borys, Ann Marie (28 березня 2014). Vincenzo Scamozzi and the Chorography of Early Modern Architecture. Ashgate Publishing. с. 140–148 and passim. ISBN 978-1-4094-5580-6.
  30. Beckh, Matthias (2015). Hyperbolic Structures: Shukhov's Lattice Towers – Forerunners of Modern Lightweight Construction. John Wiley & Sons. с. 75 and passim. ISBN 978-1-118-93268-1.
  31. The Nijni-Novgorod exhibition: Water tower, room under construction, springing of 91 feet span. The Engineer. 19 березня 1897. с. 292–294.
  32. Graefe, Rainer (1990). Vladimir G. Suchov 1853–1939. Die Kunst der sparsamen Konstruktion. Deutsche Verlags-Anstalt. с. 110–114. ISBN 3-421-02984-9.
  33. Rietveld Schröderhuis (Rietveld Schröder House). World Heritage Centre. ЮНЕСКО. Процитовано 13 грудня 2012.
  34. National Heritage List for England. Arnos Grove tube station. Historic England. Процитовано 24 лютого 2016.
  35. Moholy-Nagy, Laszlo; Hoffman, Daphne M. (trans.) (1938). The New Vision: Fundamentals of Design, Painting, Sculpture, Architecture. New Bauhaus Books. с. 46.
  36. Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. с. 306. ISBN 978-0-691-16528-8.
  37. Le Corbusier (2004) [1954 and 1958]. The Modulor: A Harmonious Measure to the Human Scale, Universally Applicable to Architecture and Mechanics. Birkhäuser. ISBN 3-7643-6188-3.
  38. Salingaros, Nikos. Architecture, Patterns, and Mathematics. Nexus Network Journal. Процитовано 9 жовтня 2015.
  39. Greene, Herb. Le Corbusier: Notre Dame du Haut at Ronchamp. Процитовано 5 жовтня 2015.[недоступне посилання з вересня 2019]
  40. Hanser, David A. (2006). Architecture of France. Greenwood Publishing Group. с. 211. ISBN 978-0-313-31902-0.
  41. Vanity Fair's World Architecture Survey: the Complete Results. Vanity Fair. 30 червня 2010. Архів оригіналу за 1 July 2010. Процитовано 22 липня 2010.
  42. Denver International Airport Press Kit. Denver International Airport. 2014. Архів оригіналу за 12 квітня 2015. Процитовано 5 жовтня 2015.
  43. Denver International Airport. Fenstress Architects. Процитовано 5 жовтня 2015.
  44. Biosphere. A view on cities. Процитовано 1 жовтня 2015.
  45. Hahn, Alexander J. (4 лютого 2013). Mathematical Excursions To Architecture. Inside Science. Процитовано 5 жовтня 2015.
  46. Salingaros, Nikos (2006). A Theory of Architecture. Umbau. с. 139–141.
  47. Salingaros, Nikos (2006). A Theory of Architecture. Umbau. с. 124–125.
  48. Gehry, Frank O.; Mudford, Grant; Koshalek, Richard (2009). Symphony: Frank Gehry's Walt Disney Concert Hall. Five Ties.
  49. Garcetti, Gil (2004). Iron: Erecting the Walt Disney Concert Hall. Princeton Architectural Press.
  50. Markowsky, George (January 1992). Misconceptions about the Golden Ratio. The College Mathematics Journal 23 (1). Архів оригіналу за 8 квітня 2008. Процитовано 18 лютого 2016.
  51. Taseos, Socrates G. (1990). Back in Time 3104 B.C. to the Great Pyramid. SOC Publishers.
  52. Gazale, Midhat (1999). Gnomon: From Pharaohs to Fractals. Princeton University Press.
  53. Kramrisch, Stella (1976), The Hindu Temple Volume 1 & 2, ISBN 81-208-0223-3
  54. Vibhuti Sachdev, Giles Tillotson (2004). Building Jaipur: The Making of an Indian City. с. 155–160. ISBN 978-1-86189-137-2.
  55. Ifrah, Georges (1998). A Universal History of Numbers. Penguin.
  56. Fractals in Indian Architecture. Yale University. Архів оригіналу за 6 лютого 2012. Процитовано 1 жовтня 2015.
  57. King, Anthony D. (2005). Buildings and Society: Essays on the Social Development of the Built Environment. Taylor & Francis. с. 72. ISBN 0-203-48075-9.
  58. Norwich, John Julius (2001). Great Architecture of the World. Artists House. с. 63.
  59. Penrose, Francis (1973) [1851]. Principles of Athenian Architecture. Society of Dilettanti. с. ch. II.3, plate 9.
  60. Stevens, Gorham P. (July 1962). Concerning the Impressiveness of the Parthenon. American Journal of Archaeology 66 (3). с. 337–338. doi:10.2307/501468.
  61. Начала Евкліда
  62. Archibald, R. C. Notes on the Logarithmic Spiral, Golden Section and the Fibonacci Series. Процитовано 1 жовтня 2015.
  63. Applications of the Golden Mean to Architecture
  64. Markowsky, George (January 1992). Misconceptions about the Golden Ratio. The College Mathematics Journal 23 (1). Архів оригіналу за 8 квітня 2008. Процитовано 18 лютого 2016.
  65. Gedal, Najib. The Great Mosque of Cordoba: Geometric Analysis. Islamic Art & Architecture. Архів оригіналу за 2 жовтня 2015. Процитовано 16 жовтня 2015.
  66. Irwin, Robert (26 травня 2011). The Alhambra. Profile Books. с. 109–112. ISBN 1-84765-098-8.
  67. Robertson, Ann (2007). Revisiting the Geometry of the Sala de Dos Hermanas. BRIDGES. Процитовано 11 жовтня 2015.
  68. Blair, Sheila; Bloom, Jonathan M. (1995). The Art and Architecture of Islam 1250–1800. Yale University Press. ISBN 0-300-06465-9.
  69. Michell, George; Pasricha, Amit (2011). Mughal Architecture & Gardens. Antique Collectors Club. ISBN 978-1-85149-670-9.
  70. Koch, Ebba (2006). The Complete Taj Mahal: And the Riverfront Gardens of Agra (вид. 1st). Thames & Hudson. с. 24 and passim. ISBN 0-500-34209-1.
  71. Koch, Ebba (2006). The Complete Taj Mahal: And the Riverfront Gardens of Agra (вид. 1st). Thames & Hudson. с. 104–109. ISBN 0-500-34209-1.
  72. Fazio, Michael; Moffett, Marian; Wodehouse, Lawrence (2009). Buildings Across Time (вид. 3rd). McGraw-Hill Higher Education. ISBN 978-0-07-305304-2.
  73. Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. с. 48. ISBN 978-0-691-16528-8.
  74. Kleiner, Fred S.; Mamiya, Christin J. (2008). Gardner's Art Through the Ages: Volume I, Chapters 1–18 (вид. 12th). Wadsworth. с. 329. ISBN 0-495-46740-5.
  75. Menander, Hanna; Brandt, Olof; Appetechia, Agostina; Thorén, Håkan (2010). The Lateran Baptistery in Three Dimensions. Swedish National Heritage Board. Процитовано 30 жовтня 2015.
  76. The Baptistery. The Leaning Tower of Pisa. Процитовано 30 жовтня 2015.
  77. Huyser-Konig, Joan. Theological Reasons for Baptistry Shapes. Calvin Institute of Christian Worship. Процитовано 30 жовтня 2015.
  78. Kuehn, Regina (1992). A Place for Baptism. Liturgy Training Publications. с. 53–60. ISBN 978-0-929650-00-5.
  79. Augustine of Hippo (426). The City of God. с. Book 22, Chapter 30.
  80. Kleiner, Fred (2012). Gardner's Art through the Ages: A Global History. Cengage Learning. с. 355–356. ISBN 1-133-71116-2.
  81. Simitch, Andrea; Warke, Val (2014). The Language of Architecture: 26 Principles Every Architect Should Know. Rockport Publishers. с. 191. ISBN 978-1-62788-048-0.
  82. Zelená hora near Žďár nad Sázavou. Czech Tourism. Процитовано 10 листопада 2015.
  83. Attributes of Saint John of Nepomuk. Saint John of Nepomuk. Архів оригіналу за 4 березня 2016. Процитовано 10 листопада 2015.
  84. Burry, M.C., J.R. Burry, G.M. Dunlop and A. Maher (2001). Drawing Together Euclidean and Topological Threads (pdf). Presented at SIRC 2001 – the Thirteenth Annual Colloquium of the Spatial Information Research Center. Dunedin, New Zealand: University of Otago. Архів оригіналу за 31 жовтня 2007. Процитовано 28 листопада 2007.
  85. The Geometry of Antoni Gaudi. Math & the Art of MC Escher. Saint Louis University Mathematics and Computer Science. Процитовано 4 жовтня 2015.
  86. Usvat, Liliana. Antony Gaudi and Mathematics. Mathematics Magazine. Процитовано 4 жовтня 2015.
  87. M.C. Burry; J.R. Burry; G.M. Dunlop; A. Maher (2001). Drawing Together Euclidean and Topological Threads. The 13th Annual Colloquium of the Spatial Information Research Centre, University of Otago, Dunedin, New Zealand. Архів оригіналу за 25 червня 2008. Процитовано 5 серпня 2008.
  88. Nervi, Pier Luigi. Cathedral of Saint Mary of the Assumption. Architectuul. Процитовано 12 жовтня 2015.
  89. Brasilia Cathedral. About Brasilia. Процитовано 13 листопада 2015.
  90. Behrends, Ehrhard; Crato, Nuno; Rodrigues, Jose Francisco (2012). Raising Public Awareness of Mathematics. Springer Science & Business Media. с. 143. ISBN 978-3-642-25710-0.
  91. Emmer, Michele (2012). Imagine Math: Between Culture and Mathematics. Springer Science & Business Media. с. 111. ISBN 978-88-470-2427-4.
  92. Mkrtchyan, Ruzanna (2013). Cathedral of Brasilia. Building.AM. Процитовано 13 листопада 2015.
  93. Rønning, Frode. Islamic Patterns And Symmetry Groups. University of Exeter. Процитовано 18 квітня 2014.
  94. Gibberd, Matt; Hill, Albert (20 серпня 2013). The Return of Ornamentation. The Telegraph. Процитовано 12 жовтня 2015.
  95. Ravensbourne College by Foreign Office Architects. de zeen magazine. 13 вересня 2010. Процитовано 12 жовтня 2015.
  96. Bizley, Graham. FOA's peninsula patterns for Ravensbourne College. bdonline.co.uk. Процитовано 16 жовтня 2015.
  97. Duffy, C. (1975). Fire & Stone, The Science of Fortress Warfare 1660–1860. Booksales. ISBN 978-0-7858-2109-0.
  98. Chandler, David (1990). The Art of Warfare in the Age of Marlborough. Spellmount. ISBN 978-0-946771-42-4.
  99. Giedion, Siegfried (1962) [1941]. Space, Time and Architecture. Harvard University Press. с. 43.
  100. Mahdavinejad, M.; Javanrudi, Kavan (July 2012). Assessment of Ancient Fridges: A Sustainable Method to Storage Ice in Hot-Arid Climates. Asian Culture and History 4 (2). doi:10.5539/ach.v4n2p133.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.