Патерни у природі

Патерни у природі — це видима регулярність форм природного світу. Ці патерни утворюються у різних контекстах та деколи можуть були змодельовані математично. До природних патернів належать симетрії, дерева, спіралі, меандри, хвилі, піни, теселяції, тріщини та стрічки[1].

Природні патерни формуються під дією вітру на пісок у дюнах пустелі Наміб. Бархани у формі півмісяця та зиб на їх поверхні повторюються за сприятливих умов.
Патерни на єменському хамелеоні, які еволюціонували для камуфляжу та сигналізації настрою та стан для спарювання.

Давньогрецькі філософи вивчали патерни; Платон, Піфагор та Емпедокл намагались пояснити їх природу. Сучасне розуміння видимих патернів розвивалось з плином часу. У 19-му ст., бельгійській фізик Жозеф Плато вивчав мильну плівку та сформулював концепцію мінімальної поверхні. Німецький біолог та митець Ернст Геккель змалював сотні морських організмів для підкреслення їх симетрії. Шотландський біолог Д'арсі Томпсон став першим у дослідженні патернів зростання у рослин та тварин, продемонструвавши, що прості рівняння можуть пояснити спіральне зростання. У 20-му сторіччі, британський математик Алан Тюрінг передбачив механізми морфогенезу, які спричиняють патерни плям та стрічок (напр. на тиграх). Угорський біолог Арістид Лінденмаєр та франко-американський математик Бенуа Мандельброт продемонстрували, як математика фракталів може створювати патерни зростання рослин.

Математика, фізика та хімія можуть пояснити природні патерни на різних рівнях. Патерни у живих організмах пояснюються біологічними процесами природного та статевого добору. Дослідження формування патернів використовують цифрове моделювання для симуляції формування широкої кількості патернів.

Історія
Патерни Фібоначчі поширені у рослинних структурах, у тому числі на цій шишці Cycas circinalis

Давньогрецькі філософи намагалися пояснити порядок у природі. Платон — якщо розглядати лише його праці про природні патерни — доводив існування універсалів. Він вважав, що вони складаються з ідеальних форм (εἶδος ейдос: «форма»), а фізичні об'єкти є лише їх недосконалі копії. Тому квітка може мати грубу форму кола, але ніколи не буде ідеальним математичним колом[2]. Піфагор пояснював патерни у природі як музичні гармонії, що виникають з числа, як для нього було складовою всесвіту[3]. Емпедокл певним чином випередив еволюційне пояснення Дарвіна для структур організмів[4]

Леонардо Фібоначчі 1202 року ознайомив західний світ з послідовністю Фібоначчі у своєму трактаті «Книга абака»[5]. Фібоначчі навів (нереалістичний) біологічний приклад про зростання теоретичної популяції кролів[6]. 1917 року Д'Арсі Вентворт Томпсон надрукував свою книгу «On Growth and Form» (Про зростання та форму), в якій описані філотаксис та послідовність Фібоначчі, математичні зв'язки у спіральних патернах зростання у рослин, які стали класикою. Він продемонстрував, що прості рівняння можуть пояснити всі візуально складні патерни зростання рогів тварин та мушель молюсків[7].

Бельгійській фізик Жозеф Плато у 19 ст. сформулював математичну проблему існування мінімальної поверхні в конкретних межах, яка зараз носить його назву. Він досліджував мильні бульбашки, та сформулював закони Плато, які описують структури, які формують плівки у піні[8].

Німецький психолог 19-го ст. Адольф Цайзінг стверджував, що золотий перетин виражений у розташуванні частин рослин, у скелетах тварин та патернах розташування їх кровоносних вен та нервів, а також у геометрії кристалів[9][10][11].

Ернст Геккель намалював прекрасні ілюстрації морських організмів, зокрема радіолярій, підкреслюючи їх симетрію на підтримку своїх псевдодарвінівських теорій еволюції[12].

Американський фотограф початку 20-го ст. Вільсон Бентлі зробив першу мікрофотографію сніжинки 1885 року[13].

Д'Арсі Томпсон був піонером вивчення зростання та форми в своїй книзі 1917 р.

1952 року Алан Тюрінг (1912—1954), краще відомий своїми роботами з програмування та криптоаналізу, написав «The Chemical Basis of Morphogenesis» (Хімічна основа морфогенезу), аналіз механізмів, потрібних для створення патернів у живих організмах, у процесі морфогенезу[14]. Він передбачив хімічні реакції, зокрема реакцію Бєлоусова — Жаботинського. На думку Тюрінга, ці механізми активації-інгібіції можуть створювати патерни смужок та плям у тварин, та вносити вклад у спіральні патерни рослинного філотаксису[15].

1968 року угорський теоретичний біолог Арістид Лінденмаєр розробив L-системи, формальну граматику, яка може бути використана для моделювання патернів зростання рослин у стилі фракталів.[16] L-системи мають абетку символів, що можуть з використанням правил виробництва бути поєднані у більші набори символів, та механізм для перетворення створених наборів символів у геометричні фігури. Після століть повільного розвитку математики патернів у роботах таких авторів як Ґотфрід Вільгельм Лейбніц, Георг Кантор, Гельґе фон Кох, Вацлав Серпінський та інших, Бенуа Мандельброт 1975 року написав відому працю «How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension» (Яка довжина узбережжя Британії? Статистична самоподібність та дробова розмірність), узагальнивши математичну думку у концепцію фрактала.[17]

Причини
Складні патерни: Попелиці та їх молодняк у кластерах на листі платана, поділеному на многокутники жилками, яких уникають молоді попелиці

Живі організми, такі як орхідеї, колібрі та хвіст павича мають абстрактний дизайн з красою форми, патерну та кольору, які митці намагаються відтворити[18]. Краса, яку людина бачить у природі, має походження на різних рівнях, у тому числі у математиці, яка визначає, які патерни можуть взагалі утворитися, а середи живих організмів — ще і у наслідках природного відбору, які визначають, які патерни еволюціонують[19]/

Математика намагається відкрити та пояснити абстрактні патерни або повторювання всіх видів[20][21]. Візуальні патерни у природі пояснюються теорією хаосу, фракталами, логарифмічними спіралями, топологією та іншими математичними патернами. Наприклад, L-системи формують переконливі моделі різних патернів зростання дерев[16].

Патерни зростання певних дерев нагадують ці фрактали системи Лінденмаєра.

Закони фізики застосовують абстракції математики до реального світу, часто за припущення, що він ідеальний. Наприклад, кристал є ідеальним, якщо у ньому не має структурних дефектів, наприклад дислокацій, та він повністю симетричний. Точна математична модель може лише наближатись до реальних об'єктів[22]. Видимі патерни у природі підпорядковуються законам фізики; наприклад, меандри можна пояснити динамікою рідин.

У біології, природний добір може спричинити розвиток патернів у живих організмах з декількох причин, включаючи камуфляж[23], статевий добір[23] та різні види сигналізації, у тому числі мімікрію[24] та симбіоз чищення[25]. У рослинах, форми, кольори та патерни квіток таких як лілія розвинулись для оптимізації комахозапилення (інші рослини можуть запилюватись вітром, птахами чи кажанами). Бджола медоносна та інші запилюючі комахи приваблюються до квіток радіальним патерном кольорів та смужок (деякі видимі лише в ультрафіолеті), які слугують вказівкою шляху до нектару, видимою здалека; запахом; та винагородою у вигляді багатого на цукри нектару та їстівного пилку[26].

Типи патернів

Симетрія
Докладніше: Симетрія (біологія), Квіткова симетрія і Кристалічна структура

Симетрія присутня повсюди серед живих організмів. Тварини переважно мають двосторонню або осьову симетрію, так само як листя рослин та деякі квіти, наприклад орхідні[27]. Рослини часто мають радіальну або обертальну симетрію, так само як багато квітів та деякі групи тварин, напр. актинії. П'ятикратна симетрія присутня у голкошкірих, групи, яка включає морські зірки, морські їжаки та морські лілії[28].

Серед неживих речей, сніжинки мають вражаючу шестикратну симетрію: кожна сніжинка унікальна — її структура є записом різних умов протягом її кристалізації, з майже однаковим патерном зростання на всіх 6 гілках[29].Кристали в цілому мають багато симетрій та габітусів; вони можуть бути кубічні чи октаедральні, але справжні кристали не можуть мати п'ятикратну симетрію (на відміну від квазікристалів)[30]. Обертальну симетрію можна побачити серед неживих речей на різних масштабах, у тому числі схожій на корону формі сплеску, який утворюється на поверхні при падінні краплі у ставок[31], та у сфероїдній формі і кільцях таких планет як Сатурн[32].

Симетрія має декілька причин. Радіальна симетрія корисна для таких організмів, як морські анемони, чиї дорослі форми не рухаються: їжа та загрози можуть приплисти з будь-якого напрямку. А тварини, які рухаються в одному напрямку за необхідністю мають верхню та нижню частини, передню та задню частини, та відповідно ліву та праву. Передня частина стає головою — спеціалізованим органом з ротом та органами чуття (цефалізація), а тіло стає двосторонньо симетричним (хоча внутрішні органи не обов'язково)[33]. Більш загадкові є причини для п'ятикратної (пентарадіальної) симетрії голкошкірих. Ранні голкошкірі були двосторонньо симетричні, а їх личинки досі є. Сумрал та Рей доводять, що втрата попередньої симетрії мала еволюційні та екологічні причини[34].

  • Тварини часто мають дзеркальну або двосторонню симетрію, як цей тигр.
  • Голкошкірі, які ця морська зірка, мають п'ятикратну симетрію.
  • П'ятикратну симетрію можна побачити у багатьох квіток та деяких плодів, як цей чишкун.
  • Сніжинки мають шестикратну симетрію.
  • Кожна сніжинка унікальна, але симетрична.
  • Флюорит демонструє кубічний габітус
  • Водяний сплеск нагадує радіальну симетрію.
  • Кристал гранату демонструє габітус ромбічного додекаедра
  • Вольвокс має сферичну симетрію.
  • Морські анемони мають обертальну симетрію.

Дерева, фрактали

Фрактали — це нескінченно самоподібні, повторювані математичні конструкції, які мають фрактальну розмірність[17][35][36] Нескінченні ітерації у природі неможливі, тому всі «фрактальні» патерни є лише наближенням. Наприклад, листа папороті та зонтичних самоподібні лише до 2, 3 чи 4 рівня. Схожі на папороть патерни зростання трапляються у рослинах та тваринах, включно з можуватками, коралами, гідроїдними (напр. Sertularia argentea) та у неживих речах, найбільш відомо — при електричному розряді. Системні фрактали Лінденмаєра можуть моделювати різні патерни зростання дерев шляхом зміни невеликої кількості параметрів, у тому числі кут росту гілки, відстань між гілками та кількість гілок на точку росту[16].

Схожі на фрактали патерни широко зустрічаються у природі — у хмарах, мережі річок, геологічних скидах, горах, узбережжях[37], забарвленні тварин, сніжинках[38], кристалах[39], системі кровоносних судин[40] та океанських хвилях[41].

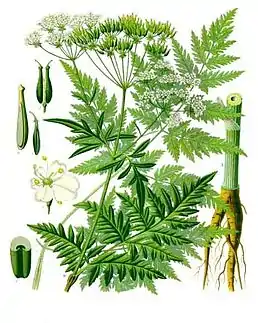  • Листя Anthriscus sylvestris має два чи три рівні самоподібності, а не нескінченні
  • Фрактальні спіралі: самоподібність капусти Романеско
  • Самоподібне суцвіття дягелю
  • Дерева: Фігура Ліхтенберга: високовольтне діелектричне розгалуження у блоку з акрилового полімеру
  • Дерева: дендритні кристали міді (під мікроскопом)
  • Фрактальні патерни розмерзання на Марсі

Спіралі
Докладніше: Філотаксис

Спіралі є поширеними у рослин та у деяких тварин, переважно молюсків. Наприклад, у наутилуса, головоногого молюска, кожне відділення мушлі є приблизною копією наступного, з масштабуванням на постійний фактор та розташуванням у логарифмічній спіралі.[42] враховуючи сучасне розуміння фракталів, спіраль зростання може розглядатись як особливий випадок самоподібності[43].

Рослинні спіралі можна побачити у філотаксисі, розташуванні листя на стеблі, та у розташуванні (парастиха[44]) інших частин рослин, наприклад квіток у айстрових чи насіннєвої головки у соняшника чи структури плодів у ананаса[45] чи пальми салак, а також у патернах лушпиння соснових шишок, де численні спіралі розташовані одночасно у напрямку за та проти годинникової стрілки. Такі розташування мають пояснення на різних рівнях — математики, фізики, хімії, біології — кожне з яких поодинці правильне, але необхідні всі разом[46]. Спіралі філотаксису можна математично вивести зі ряду Фібоначчі 1, 1, 2, 3, 5, 8, 13… (кожне наступне число — сума двох попередніх). Наприклад, коли листя чергується на стеблі, один оборот спіралі торкається двох листків, тому патерн має співвідношення 1/2. У ліщини співвідношення становить 1/3; у абрикоса — 2/5; у груші — 3/8; у мигдаля — 5/13.[47] У дисковому філотаксисі, наприклад у соняшника чи ромашки, квіточки розташовані по спіралі Ферма з числами Фібоначчі, коли квітка повністю розквітла і всі її елементи одного розміру. Співвідношення Фібоначчі наближаються до золотого кута, 137,508°, який визначає кривину спіралі Ферма[48]

З точки зору фізики, спіралі є конфігурацією з найменшою енергією[49], які спонтанно поєднуються у процесі самоорганізації в динамічних системах[50]. З точки зору хімії, спіраль може утворитись в процесі реакції-дифузії, який включає і активацію, і пригнічення. Філотаксис контролюється білками, які управляють концентрацією рослинного гормону ауксина, що активує зростання меристеми, разом з іншими механізмами, які контролюють відносний кут бруньок довкола стебла[51]. З біологічної точки зору, природний відбір надає перевагу розташуванню листя якнайдалі одне від одного в межах можливого у будь-якому просторі, оскільки це максимізує доступ до ресурсів, особливо сонячного світла для фотосинтезу.[45]

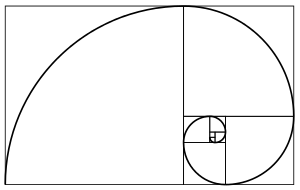  • Спіраль Фібоначчі
  • Товсторіг
  • Спіраль: філотаксис Aloe polyphylla
  • Логарифмічна спіраль зростання мушлі молюска наутілус
  • Спіраль Ферма: голівка соняшника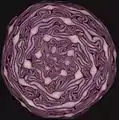
  • Численні спіралі Фібоначчі: розріз червоної капусти
  • Мушдя молюска-гастропода, Trochoidea liebetruti, демонструє рух отвору довкола, назовні та вниз по мірі зростання

Хаос, потік, меандри

У математиці, динамічна система є хаотичною, якщо вона (сильно) чутлива до початкових умов (так званий «ефект метелика»[52]), що вимагає математичні характеристики топологічного перемішування та щільних періодичних орбіт[53].

Крім фракталів, теорія хаосу також є одним з універсальних впливів на патерни у природі. Існує зв'язок між хаосом та фракталами — дивні атрактори у хаотичних системах мають фрактальну розмірність[54]. Деякі клітинні автомати, прості набори математичних правил, які генерують патерни, мають хаотичну поведінку, особливо Правило 30 Стівена Вольфрама[55].

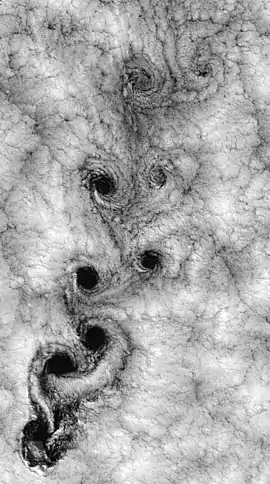
Вихрові вулиці — це патерни у формі зигзагів з вихорів, які закручуються та утворені нестабільним поділом потоку флюїда, найчастіше води чи повітря, над перешкодами.[56] Гладкий (ламінарний) потік починає розбиватися, коли розмір перешкоди або швидкість потоку стають достатньо великі у порівнянні з в'язкістю флюїда.

Меандри — це синусоподібні вигини річок чи інших каналів, які формуються, коли рідина, найчастіше вода, огинає вигини. Як тільки шлях є принаймні трошки вигнутий, величина та вигин кожного кільця зростає, оскільки спіральний потік тягне матеріал (пісок, гравій) поперек річки до внутрішньої сторони вигину. Зовнішня сторона кільця залишається чистою та незахищеною, тому ерозія зростає, далі збільшуючи процес утворення меандрів у сильному позитивному зворотньому зв'язку[57].

  • Хаос: мушля молюска-гастропода Conus textile нагадує клітинний автомат Правила 30
  • Хаос: вихрова вулиця з хмар
  • Меандри: фото з космосу на видовищні меандрові шрами та стариці на широкій заплаві Ріо Негро, Аргентина
  • Меандри: вигини річки Кауто, Куба
  • Меандри: ковзання змії
  • Меандри: симетричний корал, Diploria strigosa

Хвилі, дюни

Хвилі переносять енергію по мірі руху. Механічні хвилі поширюються середовищем — воду чи повітря, змушуючи його коливатись при їх проходженні[58] Утворені вітром хвилі на поверхні води утворюють характерний хаотичний патерн на будь якому великому вмістищі води, хоча їх статистичну поведінку можна передбачити моделями для таких хвиль[59]. Коли звилі у воді чи вітер на поверхні проходять над піском, вони утворюють патерни рябі. Коли вітри дмухнуть над великою піщаною територією, вони утворюють дюни, деколи величезні дюнні поля як у пустелі Такла-Макан. Дюни можуть утворювати декілька патернів, у тому числі напівмісяці (бархани), дуже довгі прямі лінії, зірки, куполи, параболи, та поздовжні або Саїф ('меч') форми[60].

Бархани (дюни у формі напівмісяця) утворюються у пустелі під дією вітру; два роги та внутрішня (ввігнута) сторона спрямовані проти вітру. Під дією вітру пісок піднімається по навітряній (зовнішній) стороні, яка має кут приблизно у 15° з горизонталлю, та падає на підвітряну (внутрішню) сторону, де накопичується до досягнення кута природного укосу піску (приблизно 35°). Коли кут поверхні перевищує кут природного укосу, пісок сходить лавиною, що є нелінійною поведінкою: багаторазове додання невеликих кількостей піску не викликає ніякої дії, а потім наступна невелика кількість викликає схід лавиною великої кількості піску[61]. Крім цієї нелінійності, в іншому бархани поводяться схоже на солітони[62].

  • Хвилі: хвиля при проходженні судна
  • Дюни: вид з космосу на піщані дюни пустелі Такла-Макан
  • Дюни: бархан
  • Зиб від вітру по піску з дислокацією у Сістані, Афганістан

Бульбашки, піна

Мильна бульбашка формує сферу, мінімальну поверхню — найменшу можливу поверхню довкола заданого об'єму. Дві бульбашки разом формують більш складну форму: зовнішні поверхні обох бульбашок будуть сферичними; вони будуть поєднані третьою сферичною поверхнею, коли менша бульбашка буде трохи находити на більшу[63].

Піна — це маса бульбашок; у природі трапляється піна з різних матеріалів. Піна з мильних плівок підпорядковується законам Плато, які вимагають, щоб три мильні плівки зустрічались під кутом 120°, а чотири — як чотиригранників в одній вершині з кутами бл. 109,5°. Закони Плато також вимагають, щоб плівки були гладкі та безперервні та мали постійну середню кривину у будь-якій точці. Наприклад, плівка може бути майже пласкою в середньому, якщо вона має кривину вгору в одному напрямку (наприклад зліва направо) та кривину вниз в іншому напрямку (спереду назад)[64][65].

Структури з мінімальними поверхнями можна використовувати як тенти. Вільям Томсон, лорд Кельвін, 1887 року ідентифікував проблему найбільш ефективного методу пакування одиниць однакового об'єму як піни; його рішення використовує лише одне тіло обертання, двічі усічені кубічні стільники з дуже незначно вигнутими поверхнями, для дотримання законів Плато. Краще рішення було знайдено лише 1993 року, коли Деніс Вейр та Роберт Феланза пропонували конструкцію Вейра-Фалена; Пекінський національний плавальний комплекс на Літніх Олімпійських іграх 2008 використав конструкцію для зовнішньої стіни [66].

На рівні живих клітин, пінні патерни поширені; радіолярії, спікули губок, силікофлагеллятні екзоскелети та кальцитні скелети морських їжаків, всі нагадують мінеральні зліпки плівок піни Плато[67][68]. Скелет радіолярії Aulonia hexagona, намальований Геккелем, виглядає наче сфера, повністю складена шестикутниками, але це математично неможливо. Характеристика Ейлера стверджує, що для кожного опуклого багатогранника, кількість поверхонь плюс кількість вершин має дорівнювати кількості ребер плюс 2. З дотриманням цього, будь-який закритий багатогранник, складений шестикутниками, має включати точно 12 п'ятикутників, наприклад м'яч для футболу, геодезичний купол Фуллера чи молекули фулерену[69].

  • Піна з мильних бульбашок: 4 грані зустрічаються на кожній вершині, під кутами бл. 109.5°, як дві пари C-H у метані.
  • Раддіолярії, намальовані Геккелем у його "Kunstformen der Natur" (1904).
  • Спумелярії Геккеля; скелети цих радіолярій мають форми, схожі на піну.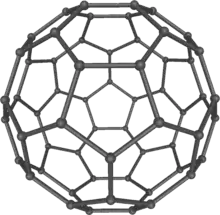
  • Buckminsterfullerene C60: Річард Смоллі з колегами синтезували молекулу фулерену 1985 року.
  • Брохосоми (секреторні мікрочасточки, які виділяють стрибунці) часто нагадують геометрію фулеренів.
  • Тент цирку нагадує мінімальну поверхню.
  • Пекінський національний плавальний комплекс має поверхню Вейра-Фалена.
  • Однакові сфери (газові бульбашки) на поверхневій піні

Теселяції

Теселяції — це патерни, сформовані повторенням «мозаїки» по всій пласкій поверхні. Існує всього 17 шпалерних груп такого поділу[70]. Хоча у мистецтві та дизайні вони поширені, точно повторювані поділи досить важко побачити у живих організмах. Відомими прикладами є секції у «паперових» гніздах соціальних ос та воскові секції у бджолиних стільниках. У тварин, кістяні риби, рептилії та панголіноподібні, чи у таких фруктів як салак, де існує захисний шар з насунутих одна на одну лушпайок чи остеодермів, такий шар утворює щось схоже на повторювані патерни, хоча насправді лушпайки постійно змінюються у розмірі. Серед квітів, рябчик шаховий має на пелюстках тесельований малюнок, схожий на шахівницю.

Структури мінералів дають добрий приклад постійно повторюваних тривимірних ґраток. Незважаючи на тисячі відомих мінералів, існує лише небагато можливих типів розташування атомів у кристал, що визначається кристалічною структурою, сингонією та точковою групою; наприклад, існує лише ґраток Браве для 7 систем ґраток у тривимірному просторі[71]

  • Кристали: кубічні кристали галіту (кам'яної солі); кубічна сингонія, ізометрична гексооктаедральна кристальна симетрія
  • Ряди: Бджолині стільники - це природна теселяція
  • Кристал бісмута демонструє сходинковий габітус.
  • Поділ: тесельована квітка рябчика шахового
  • Поділ: наповзаючі лушпайки плітки звичайної
  • Поділ: наповзаючі лушпайки фрукта салак
  • Тесельоване замощення: рідкісне скельне утворення на півострові Тасман

Тріщини

Тріщини — це лінійні отвори, які утворюються в матеріалах для зняття стресу. Коли еластичний матеріал розтягується або стискається узгоджено, він врешті решт сягає межі міцності на розрив і тоді раптово розривається у всіх напрямках, створюючи тріщини, з'єднані під кутами 120°, тобто з однієї точки виходять три тріщини. На противагу цьому, при розриві нееластичного матеріалу, для зняття стресу формуються прямі тріщини. Подальший стрес у тому самому напрямку просто розширить існуючі тріщини; стрес під прямим кутом до попереднього напрямку може створити нові тріщини, відповідно під кутом 90° до вже наявних. Таким чином патерн тріщин вказує на еластичність чи нееластичність матеріалу[72]. У жорстких волокнистих матеріалах, наприклад дубовій корі, тріщини для зняття стресу утворюються як звичайно, але вони не бувають дуже довгими, оскільки їх зростання переривається пучками сильних еластичних волокон. Оскільки кожен вид дерева має власну структуру на рівні клітин та молекул, вони всі мають різні патерни тріщин на корі[73].

  • Поверхня старого глазурованого посуду, де полива має переважно тріщини з кутами 90°
  • Висихаючий нееластичний бруд солоного болота Качського Ранну, Індія, з тріщинами переважно 90°
  • Габро з тріщинами 90°, поблизу Сгурр-на-Стрі, острів Скай
  • Висихаючий еластичний бруд на Сицилії з тріщинами переважно у 120°
  • Охолоджений базальт на Дорозі Гігантів. Вертикальні тріщини з кутами переважно 120°, завдяки яким утворилися шестикутні колони
  • Кора пальми з розгалуженими вертикальними тріщинами (та горизонтальними слідами від опалого листя)

Плями, смужки

Леопарди та сонечка мають плями; риби-ангели та зебри — смужки[74]. Ці патерни мають еволюційне пояснення — вони мають функції, які підвищують шанси потомства тварини з патернами на виживання та розмноження. Однією з функції патернів тварин є камуфляж[23] (леопард, якого важче побачити, вловить більше здобичі). Друга функція — сигналізування[24] — наприклад, сонечка будуть менше атаковані хижими птахами, які полюють з покладанням на зір, якщо вони мають яскраві попереджувальні кольори та неприємно гіркі чи отруйні, або нагадують інших «несмачних» комах. Молодий птах може побачити комаху з попереджуючим патерном і спробує її з'їсти, але це трапиться лише раз; птах виплюне гірку комаху, а інші сонечка на цій території залишаться неушкодженими. Молоді леопарди та сонечка, які наслідують гени плямистості, виживають. Але хоча ці еволюційні та функціональні доводи пояснюють чому цим тваринам потрібні патерни, на цей час відсутнє пояснення, як ці патерни формуються[74].

Формування патернів

Алан Тюрінг[14], а пізніше біолог-математик Джеймс Мюррей, описали механізм, який спонтанно створює патерни плям чи смужок: система реакції-дифузії[75]. Клітини молодого організму мають гени, які можуть бути активовані хімічним сигналом, — морфогеном, наслідком чого стає зростання структури певного типу, наприклад ділянки шкіри з темним пігментом. Якщо морфоген присутній всюди, результатом стане рівномірна пігментація, напр. як чорна пантера. А якщо він поширений нерівномірно, з'являться плями чи смужки. Тюрінг припустив, що може бути зворотній контроль для виробництва самого морфогена. Це може спричинити постійні коливання у кількості морфогену по мірі його поширення тілом. І необхідний другий механізм для створення патернів стоячої хвилі (утворення плям чи смужок): хімічний інгібітор, який вимкне виробництво морфогену і поширюється тілом швидше, ніж сам морфоген, утворюючи схему активатора-інгібітора. Реакція Бєлоусова — Жаботинського є небіологічним прикладом такої схеми, хімічним осцилятором[75].

Пізніші дослідження створили переконливі моделі утворення різних патернів — смужок зебри, плям жирафів, ягуарів та сонячок[76]. Моделі активації-інгібіції Річарда Прама, які використати роботу Тюрінга, використовують шість змінних для пояснення видимого діапазону 9 базових патернів пір'їни, від найпростішого, центральної пігментної плями, до складніших концентричних плям, полосок, шевронів, плям у вигляді ока, пари центральних прям, рядів подвійних плям та розсипу точок[77][78]. Більш складні моделі симулюють складні патерни пір'я у гвінейської цесарки, у якої окремі пір'їни демонструють перехід від смужок на початку пір'їни до розсипу точок на кінці. Це потребує коливання двох пригнічуючих сигналів, які взаємодіють у просторі та часі[78].

Патерни можуть формуватися з інших причин у зелених ландшафтах тигрового буша[79] та ялицевих хвиль[80]. Смужки тигрового буша виникають на сухих схилах, де зростання рослин обмежене дощовими опадами. Кожна умовно горизонтальна смуга рослинності фактично збирає дощову воду з пустельної території безпосередньо над нею[79]. Ялицеві хвилі трапляються у лісах на схилах гір після сильних вітрів, під час регенерації. Коли дерева падають, інші дерева, які вони прикривали, лишаються незахищеними, і з більшою ймовірністю теж будуть пошкоджені, тому такі просіки мають тенденцію розташовуватись «по вітру». В проти вітру ростуть молоді дерева, захищені «вітровою тінню» високих дерев, які вціліли[80]. Природні патерни деколи формуються і тваринами, наприклад у Mima mounds у північно-західній частині США та деяких інших місцях — вважається, що вони були створені протягом багатьох років закопуваннями гоферових.[81].

На вічномерзлих ґрунтах з активним верхнім шаром, який щорічно замерзає-розмерзає, може сформуватися патерн на ґрунті — кола, сітки, багатогранники з крижаними сторонами, перепади та смуги. Термальне стискання спричиняє появу тріщин стискання; під час розмерзання, тріщини заповняє вода, розширюючи їх коли крига замерзає. Ці тріщини можуть поєднуватись у багатокутники та інші форми[82].

  • Риба мбу
  • Деталь патерну шкіри риби мбу
  • Кадр з симуляції реакції Бєлоусова — Жаботинського
  • Пір'я цесарки - перехід від смужок до плям, як по пір'їнах, так і по всьому птаху
  • Вид з повітря на плато тигрового буша у Нігері
  • Ялицеві хвилі у Білих горах, Нью-Гемпшир, США
  • Патерн на землі: танучий гідролаколіт, оточений багатогранниками з крижаними сторонами, поблизу Тактояктук, Канада

Див. також

Примітки
  1. Stevens, 1974, с. 3.
  2. Balaguer, Mark (7 квітня 2009) [2004]. Stanford Encyclopedia of Philosophy. Platonism in Metaphysics. Stanford University. Процитовано 4 травня 2012.
  3. Піфагорейці вважали, що принципи математики є принципами всього сущого
  4. Арістотель писав про такі міркування Емпедокла: «де все трапилось так, наче воно траплялось з певною метою, там тварини вижили, випадково створені прийнятним чином; а де цього не трапилось, тварини вимерли.»
  5. Singh, Parmanand. Acharya Hemachandra and the (so called) Fibonacci Numbers. Math. Ed. Siwan, 20(1):28–30, 1986. ISSN 0047-6269
  6. Knott, Ron. Fibonacci's Rabbits. University of Surrey Faculty of Engineering and Physical Sciences.
  7. Про Д'Арсі.
  8. Stewart, 2011, с. 108-109.
  9. Padovan, Richard (1999). Proportion. Taylor & Francis. с. 305–306. ISBN 978-0-419-22780-9.
  10. Padovan, Richard (2002). Proportion: Science, Philosophy, Architecture. Nexus Network Journal 4 (1). с. 113–122. doi:10.1007/s00004-001-0008-7.
  11. Zeising, Adolf (1854). Neue Lehre van den Proportionen des meschlischen Körpers. preface.
  12. Ball, 2003, с. 41.
  13. Hannavy, John (2007). Encyclopedia of Nineteenth-Century Photography 1. CRC Press. с. 149. ISBN 0-415-97235-3.
  14. Turing, A. M. (1952). The Chemical Basis of Morphogenesis. Philosophical Transactions of the Royal Society B 237 (641). с. 37–72. Bibcode:1952RSPTB.237...37T. doi:10.1098/rstb.1952.0012.
  15. Ball, 2009, с. 41.
  16. Rozenberg, Grzegorz; Salomaa, Arto. The mathematical theory of L systems. Academic Press, New York, 1980. ISBN 0-12-597140-0
  17. Mandelbrot, Benoît B. (1983). The fractal geometry of nature. Macmillan.
  18. Forbes, Peter. All that useless beauty. The Guardian. Review: Non-fiction. 11 February 2012.
  19. Stevens, 1994, с. 222.
  20. Steen, L.A. The Science of Patterns. Science (journal), 240: 611—616, 1998. Summary at ascd.org
  21. Devlin, Keith. Mathematics: The Science of Patterns: The Search for Order in Life, Mind and the Universe (Scientific American Paperback Library) 1996
  22. Tatarkiewicz, Władysław. Perfection in the Sciences. II. Perfection in Physics and Chemistry, Dialectics and Humanism, vol. VII, no. 2 (spring 1980), p. 139.
  23. Darwin, Charles. On the Origin of Species. 1859, chapter 4.
  24. Wickler, W. (1968). Mimicry in plants and animals. New York: McGraw-Hill.
  25. Poulin, R.; Grutter, A.S. (1996) «Cleaning symbiosis: proximate and adaptive explanations». Bioscience 46(7): 512—517. (необхідна підписка)
  26. Koning, Ross (1994). Plant Physiology Information Website. Pollination Adaptations. Ross Koning. Процитовано May 2, 2012.
  27. Stewart, 2001, с. 48-49.
  28. Stewart, 2001, с. 64-65.
  29. Stewart, 2001, с. 52.
  30. Stewart, 2001, с. 82-84.
  31. Stewart, 2001, с. 60.
  32. Stewart, 2001, с. 71.
  33. Hickman, Cleveland P.; Roberts, Larry S.; Larson, Allan (2002). Animal Diversity. Chapter 8: Acoelomate Bilateral Animals (вид. Third). McGraw-Hill. с. 139. Архів оригіналу за травень 17, 2016. Процитовано 25 жовтня 2012.
  34. Sumrall, Colin D.; Wray, Gregory A. (January 2007). Ontogeny in the fossil record: diversification of body plans and the evolution of "aberrant" symmetry in Paleozoic echinoderms. Paleobiology 33 (1). с. 149–163. doi:10.1666/06053.1.
  35. Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley.
  36. Briggs, John (1992). Fractals:The Patterns of Chaos. Thames and Hudson. с. 148.
  37. Batty, Michael (4 квітня 1985). Fractals – Geometry Between Dimensions. New Scientist 105 (1450) (Holborn Publishing Group). с. 31.
  38. Meyer, Yves; Roques, Sylvie (1993). Progress in wavelet analysis and applications: proceedings of the International Conference "Wavelets and Applications," Toulouse, France – June 1992. Atlantica Séguier Frontières. с. 25.
  39. Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw (2000). Pattern formation in biology, vision and dynamics. World Scientific. с. 78. ISBN 9789810237929.
  40. Hahn, Horst K.; Georg, Manfred; Peitgen, Heinz-Otto (2005). Fractal aspects of three-dimensional vascular constructive optimization. У Losa, Gabriele A.; Nonnenmacher, Theo F. Fractals in biology and medicine. Springer. с. 55–66.
  41. Addison, Paul S. (1997). Fractals and chaos: an illustrated course. CRC Press. с. 44–46.
  42. Maor, Eli. e: The Story of a Number. Princeton University Press, 2009. Page 135.
  43. Ball, 2009, с. 29-32.
  44. Spiral Lattices & Parastichy. Smith College. Архів оригіналу за 26 травня 2010. Процитовано 24 вересня 2013.
  45. Kappraff, Jay (2004). Growth in Plants: A Study in Number. Forma 19: 335–354.
  46. Ball, 2009, с. 13.
  47. Coxeter, H. S. M. (1961). Introduction to geometry. Wiley. с. 169.
  48. Prusinkiewicz, Przemyslaw; Lindenmayer, Aristid (1990). The Algorithmic Beauty of Plants. Springer-Verlag. с. 101–107. ISBN 978-0-387-97297-8.
  49. Levitov LS (15 березня 1991). Energetic Approach to Phyllotaxis. Europhys. Lett. 14 (6). с. 533–9. Bibcode:1991EL.....14..533L. doi:10.1209/0295-5075/14/6/006.
  50. Douady, S; Couder, Y. (March 1992). Phyllotaxis as a physical self-organized growth process. Physical Review Letters 68 (13). с. 2098–2101. Bibcode:1992PhRvL..68.2098D. PMID 10045303. doi:10.1103/PhysRevLett.68.2098.
  51. Ball, 2009, с. 163, 249—250.
  52. Lorenz, Edward N. (March 1963). Deterministic Nonperiodic Flow. Journal of the Atmospheric Sciences 20 (2). с. 130–141. Bibcode:1963JAtS...20..130L. ISSN 1520-0469. doi:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2. Процитовано 3 червня 2010.
  53. Elaydi, Saber N. (1999). Discrete Chaos. Chapman & Hall/CRC. с. 117.
  54. Ruelle, David. Chance and Chaos. Princeton University Press, 1991.
  55. Wolfram, Stephen. A New Kind of Science. Wolfram Media, 2002.
  56. von Kármán, Theodore. «Aerodynamics». McGraw-Hill (1963): ISBN 978-0-07-067602-2. Dover (1994): ISBN 978-0-486-43485-8.
  57. Lewalle, Jacques (2006). Flow Separation and Secondary Flow: Section 9.1. Lecture Notes in Incompressible Fluid Dynamics: Phenomenology, Concepts and Analytical Tools. Syracuse, NY: Syracuse University. Архів оригіналу за 29 вересня 2011. Процитовано 26 лютого 2016.
  58. French, A.P. Vibrations and Waves. Nelson Thornes, 1971.
  59. Tolman, H.L. (2008). Practical wind wave modeling. У Mahmood, M.F. CBMS Conference Proceedings on Water Waves: Theory and Experiment. Howard University, USA, 13–18 May 2008: World Scientific Publ.
  60. Types of Dunes. USGS. 29 жовтня 1997. Процитовано 2 травня 2012.
  61. Strahler, A. & Archibold, O.W. Physical Geography: Science and Systems of the Human Environment. John Wiley, 4th edition 2008. Page 442.
  62. Schwämmle, V.; Herrman, H.J. (2003). Solitary wave behaviour of sand dunes. Nature 426 (Dec. 11). с. 619–620 Abstract. Bibcode:2003Natur.426..619S. PMID 14668849. doi:10.1038/426619a.
  63. Stewart, 2001, с. 108-109.
  64. Ball, 2009, с. 68.
  65. Frederick J. Almgren, Jr. and Jean E. Taylor, The geometry of soap films and soap bubbles, Scientific American, vol. 235, pp. 82–93, July 1976.
  66. Ball, 2009, с. 73-76.
  67. Ball, 2009, с. 96-101.
  68. Brodie, Christina (February 2005). Geometry and Pattern in Nature 3: The holes in radiolarian and diatom tests. Microscopy-UK. Процитовано 28 травня 2012.
  69. Ball, с. 51.
  70. Armstrong, M.A. (1988). Groups and Symmetry. New York: Springer-Verlag.
  71. Hook, J.R.; Hall, H.E. (2010). Solid State Physics (вид. 2nd). Manchester Physics Series, John Wiley & Sons. ISBN 978-0-471-92804-1.
  72. Stevens, 1974, с. 207.
  73. Stevens, 1974, с. 208.
  74. Ball, 2009, с. 156-158.
  75. Ball, 2009, с. 159-167.
  76. Ball, 2009, с. 168-180.
  77. Rothenburg, 2011, с. 93-95.
  78. Prum, Richard O.; Williamson, Scott (2002). Reaction–diffusion models of within-feather pigmentation patterning. Proceedings Royal Society London B 269. с. 781–792. doi:10.1098/rspb.2001.1896.
  79. Tongway, D.J.; Valentin, C.; Seghieri, J. (2001). Banded vegetation patterning in arid and semiarid environments. New York: Springer-Verlag. Проігноровано невідомий параметр |last-author-amp= (довідка)
  80. D'Avanzo, C. (22 лютого 2004). Fir Waves: Regeneration in New England Conifer Forests. TIEE. Процитовано 26 травня 2012.
  81. Morelle, Rebecca. ‘Digital gophers’ solve Mima mound mystery. BBC News. Процитовано 9 грудня 2013.
  82. Permafrost: Patterned Ground. US Army Corps of Engineers. Архів оригіналу за 7 березня 2015. Процитовано 17 лютого 2015.

Бібліографія

Автори-першовідкривачі

Загальні книги
  • Adam, John A. (2006). Mathematics in Nature: Modeling Patterns in the Natural World. Princeton University Press.
  • Ball, Philip (2009). Nature's Patterns: a tapestry in three parts. 1:Shapes. 2:Flow. 3:Branches. Oxford.
  • Murphy, Pat; Neill, William (1993). By Nature's Design. Chronicle Books.
  • Rothenburg, David (2011). Survival of the Beautiful: Art, Science and Evolution. Bloomsbury Press.
  • Stevens, Peter S. (1974). Patterns in Nature. Little, Brown & Co.
  • Stewart, Ian (2001). What Shape is a Snowflake? Magical Numbers in Nature. Weidenfeld & Nicolson.

Патерни з природи (як мистецтво)
  • Edmaier, Bernard. Patterns of the Earth. Phaidon Press, 2007.
  • Macnab, Maggie. Design by Nature: Using Universal Forms and Principles in Design. New Riders, 2012.
  • Nakamura, Shigeki. Pattern Sourcebook: 250 Patterns Inspired by Nature.. Books 1 and 2. Rockport, 2009.
  • O'Neill, Polly. Surfaces and Textures: A Visual Sourcebook. Black, 2008.
  • Porter, Eliot, and Gleick, James. Nature's Chaos. Viking Penguin, 1990.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.