Окружність

У геометрії, окружністю (від латинського circumferentia, що означає «обійти довкола») кола це лінійна довжина довкола нього.[1] Тобто, окружність визначає довжину кола, якби його випрямили і розтягнули в вигляді прямого відрізка. Оскільки коло це зовнішня межа круга (диску), окружність це особливий випадок периметра.[2] Периметр це довжина довкола будь-якої замкненої фігури і цей термін застосовують до всіх фігур окрім кола і подібних округлих фігур, таких як Еліпси.

Крім того, слово «окружність» може стосуватися самої межі кола, а не поняття довжини цієї межі.

Окружність кола

Ілюстрація кола з окружністю (C) показаною чорним, діаметром (D) блакитним, радіусом (R) червоним, із центром у точці (O), що виділена фіолетовим. Окружність =

π

× діаметр = 2 ×

π

× радіус.

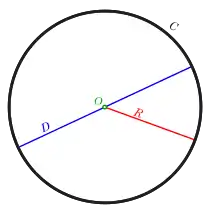
Окружність кола, це відстань довкола нього, але якщо, як у більшості елементарних трактуваннях, відстань визначається по прямій лінії, таке пояснення не може використовуватися як визначення. З таких міркувань, окружність кола можна визначити як границю периметрів вписаних правильних багатокутників із нескінченним збільшенням кількості їх сторін.[3] Поняття окружності використовують при вимірювання фізичних об'єктів, також при розгляді абстрактних геометричних форм.

Якщо діаметр кола дорівнює 1, його окружність дорівнює

π

.

Якщо радіус кола дорівнює 1, що називається одиничним колом—його окружність становить 2

π

.

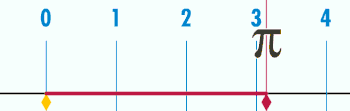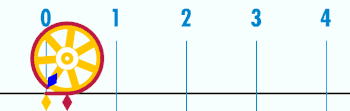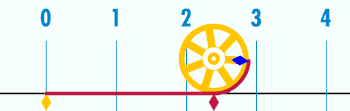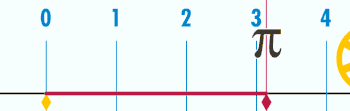
Зв'язок із числом $π$

Окружність кола пов'язана з однією з найважливіших математичних констант. Ця константа, пі, позначається грецькою літерою $π$ . Першими декількома десятковими цифрами чисельного значення $π$ є 3,141592653589793… (див. A000796). $π$ визначається як відношення довжини окружності кола $C$ до його діаметру $d$ :

\pi ={\frac {C}{d}}.

Або, аналогічним способом, як відношення довжини окружності до двох радіусів. Вищезгадану формулу можна виразити так, щоб знаходити окружність:

{C}=\pi \cdot {d}=2\pi \cdot {r}.\!

Математична константа $π$ широко використовується в математиці, техніці, і науці.

У своїй праці Вимірювання кола, написаній 250 до н.е., Архімед показав, що відношення ( $C / d$ , хоча він тоді не використовував назву $π$ ), є більшим за 31071 але меншим за 317 розраховуючи периметри вписаного і описаного правильного полігону із 96 сторонами.[4] Цей метод наближення значення $π$ використовувався століттями, що дозволяло отримувати більшої точності використовуючи полігони з усе більшою і більшою кількістю сторін. Останній подібний розрахунок в 1630 виконав Крістоф Гріенбергер, що використав полігони із 10⁴⁰ сторонами.

Окружність еліпса

Термін окружність використовується іноді для визначення периметру еліпса. Не існує загальної формули для визначення окружності еліпса через велику і малу піввісі еліпса, яка б використовувала лише елементарні функції. Однак, для цих параметрів існують наближені формули. Однією з таких апроксимацій, є формула Ейлера (1773), для конічного еліпса,

{\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,

це

C_{\rm {ellipse}}\sim \pi {\sqrt {2(a^{2}+b^{2})}}.

Деякими нижніми і верхніми межами окружності конічного еліпса із $a\geq b$ є наступні[5]

C\leq 2\pi a,

\pi (a+b)\leq C\leq 4(a+b),

4{\sqrt {a^{2}+b^{2}}}\leq C\leq \pi {\sqrt {2(a^{2}+b^{2})}}.

Тут верхньою межею $2\pi a$ є окружність описаного концентричного кола, що проходить через крайні точки великої піввісі еліпса, а нижньою межею $4{\sqrt {a^{2}+b^{2}}}$ є периметр вписаного ромба із вершинами, що лежать на крайніх точках великої і малої півосей.

Окружність еліпса можна точно виразити за допомогою повного еліптичного інтегралу другого роду.[6] Більш точно, ми будемо мати

C_{\rm {ellipse}}=4a\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta ,

де, знову ж таки, $a$ є довжиною великої піввісі і $e$ є ексцентриситетом ${\sqrt {1-b^{2}/a^{2}}}.$

Окружність графу

В теорії графів окружність графу відноситься до найдовшого (простого) циклу, що міститься в графі.[7]

Примітки

San Diego State University (2004). Perimeter, Area and Circumference. Addison-Wesley. Архів оригіналу за 6 жовтня 2014.
Bennett, Jeffrey; Briggs, William (2005). Using and Understanding Mathematics / A Quantitative Reasoning Approach (вид. 3rd). Addison-Wesley. с. 580. ISBN 978-0-321-22773-7.
Jacobs, Harold R. (1974). Geometry. W. H. Freeman and Co. с. 565. ISBN 0-7167-0456-0.
Katz, Victor J. (1998). A History of Mathematics / An Introduction (вид. 2nd). Addison-Wesley Longman. с. 109. ISBN 978-0-321-01618-8.
Jameson, G.J.O. (2014). Inequalities for the perimeter of an ellipse. Mathematical Gazette 98: 227–234. doi:10.2307/3621497.
Almkvist, Gert; Berndt, Bruce (1988). Gauss, Landen, Ramanujan, the arithmetic-geometric mean, ellipses, $π$ , and the Ladies Diary. American Mathematical Monthly 95: 585–608. MR 966232.
Harary, Frank (1969). Graph Theory. Addison-Wesley. с. 13. ISBN 0-201-02787-9.

Посилання

Numericana — Circumference of an ellipse (англ.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] San Diego State University (2004). Perimeter, Area and Circumference. Addison-Wesley. Архів оригіналу за 6 жовтня 2014.

[2] Bennett, Jeffrey; Briggs, William (2005). Using and Understanding Mathematics / A Quantitative Reasoning Approach (вид. 3rd). Addison-Wesley. с. 580. ISBN 978-0-321-22773-7.

[3] Jacobs, Harold R. (1974). Geometry. W. H. Freeman and Co. с. 565. ISBN 0-7167-0456-0.

[4] Katz, Victor J. (1998). A History of Mathematics / An Introduction (вид. 2nd). Addison-Wesley Longman. с. 109. ISBN 978-0-321-01618-8.

[5] Jameson, G.J.O. (2014). Inequalities for the perimeter of an ellipse. Mathematical Gazette 98: 227–234. doi:10.2307/3621497.

[6] Almkvist, Gert; Berndt, Bruce (1988). Gauss, Landen, Ramanujan, the arithmetic-geometric mean, ellipses, $π$ , and the Ladies Diary. American Mathematical Monthly 95: 585–608. MR 966232.

[7] Harary, Frank (1969). Graph Theory. Addison-Wesley. с. 13. ISBN 0-201-02787-9.