Теорема Тейлора
Теорема Тейлора дає наближення до функції, що диференціюється k раз, поблизу даної точки за допомогою многочлена Тейлора k-го порядку. Для аналітичних функцій многочлен Тейлора в даній точці є кінцевою послідовністю їх неповного ряду Тейлора, який, у свою чергу, повністю визначає функцію в деякому околі точки. Точний зміст теореми Тейлора до теперішнього часу не узгоджено. Звичайно, існує кілька версій теореми, що застосовуються в різних ситуаціях, і деякі з цих версій містять оцінки помилки, що виникає при наближенні функції за допомогою многочлена Тейлора.
| Розділи в | ||||||
| Математичному аналізі | ||||||
|---|---|---|---|---|---|---|
|
||||||
|
||||||
|
||||||
|
||||||
|
Спеціалізовані |
||||||
- Ця стаття про многочлени Тейлора диференційовних функцій. Про ряди Тейлора аналітичних функцій див. відповідну статтю.
Ця теорема названа на честь математика Брука Тейлора, який сформулював одну з її версій в 1712 році. Явний вираз для помилки наближення було дано набагато пізніше Жозефом Лагранжем. Раніше, в 1671 році, Джеймсом Грегорі вже було згадано наслідок з теореми.
Теорема Тейлора дозволяє опанувати прийомами обчислень початкового рівня, і вона є одним з центральних елементарних інструментів у математичному аналізі. При вивченні математики вона є початковою точкою для вивчення асимптотичного аналізу. Теорема також використовується в математичній фізиці. Вона також узагальнює аналіз функцій декількох змінних і векторні функції f : Rn → Rm для будь-яких вимірів n і m. Це узагальнення теореми Тейлора є базовим для визначення так званих струменів, які з'являються в диференціальній геометрії й в теорії диференціальних рівнянь з частинними похідними.
Передумови для введення теореми
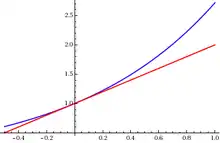
Якщо дійснозначна функція f(х) є диференційованою в точці a, то вона має лінійне наближення в точці a. Це означає, що існує функція h1 така, що
Тут
це лінійне наближення функції f в точці a. Графік функції y = P1(x) є дотичною до графіку функції f в точці x = a. Помилка наближення є такою
Помітимо, що помилка наближається до нуля трохи скоріше, ніж різниця x − a наближається до нуля відповідно до того як x прагне до a.
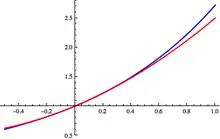
Якщо ми шукаємо краще наближення f, ми можемо використовувати многочлен другого ступеня замість лінійної функції. Замість знаходження похідної від f в точці a, ми можемо знайти дві похідні, отримавши таким чином многочлен, який так само як і f зростає (або убуває), і так само як і f має опуклість (або увігнутість) в точці a. Многочлен другого ступеня (квадратний многочлен) в цьому випадку буде виглядати наступним чином:
Теорема Тейлора дозволяє переконатися, що квадратичне наближення, в досить малому околі точки a, є кращим наближенням, ніж лінійне. Зокрема,
Тут помилка наближення така
що, за умови обмеженості h2, наближається до нуля швидше, ніж наближається до нуля (x − a)2 відповідно до того як x прагне до a.
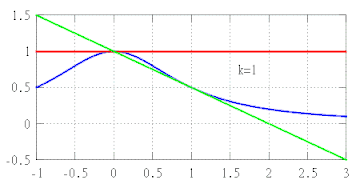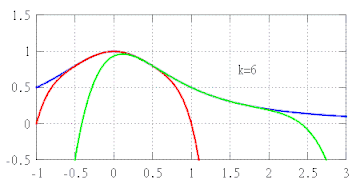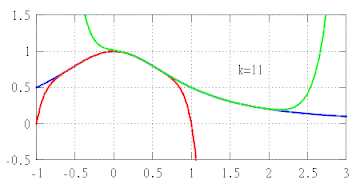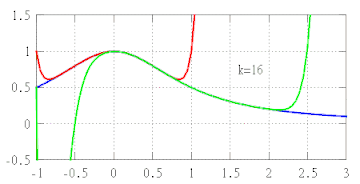
Таким чином, якщо використовувати многочлени все вищого ступеня, то будуть отримані все кращі наближення до f. Загалом, помилка в наближенні функції за допомогою поліномів порядку k буде наближатися до нуля трохи швидше, ніж наближається до нуля (x − a)k відповідно до того як x прагне до a.
Цей наслідок має асимптотичну природу: він лише повідомляє, що помилка Rk наближення за допомогою многочленів Тейлора k-го порядку Pk наближається до нуля швидше, ніж ненульовий многочлен k-го порядку відповідно до того як x → a. Він не повідомляє, наскільки великою є помилка в будь-якому околі центру наближення, але для цього існує формула для залишку (наведена нижче).
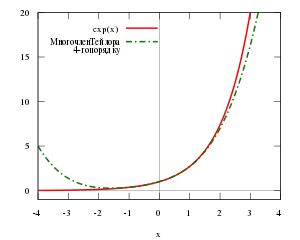
Найбільш повні версії теореми Тейлора, як правило, призводять до рівномірних оцінок помилки наближення в малому околі центра наближення, але ці оцінки не є адекватними для околів, які занадто великі, навіть якщо функція f є аналітичною. У цій ситуації слід вибирати кілька многочленів Тейлора з різними центрами наближення, щоб мати надійне Тейлорове наближення до вихідної функції (див. анімований малюнок вище). Можлива також ситуація, коли зростання порядку многочлена не збільшує якість наближення взагалі, навіть якщо функція f диференціюється нескінченну кількість разів. Такий приклад наведено нижче.
Теорема Тейлора для функцій від однієї дійсної змінної
Формулювання теореми
Точне формулювання більшості базових версій теореми наступне.
Теорема Тейлора[1] Нехай k ≥ 1 — ціле, і нехай функція f : R → R — k раз диференційовна в точці a ∈ R. Тоді існує функція hk : R → R така, що
Многочлен, що виникає в теоремі Тейлора, є многочленом Тейлора k-го порядку
функції f в точці a.
Теорема Тейлора описує асимптотичну поведінку залишкового члену
який є помилкою при знаходженні наближення функції f за допомогою многочленів Тейлора. Використовуючи «O» велике та «o» маленьке, теорему Тейлора можна сформулювати так
Формули для залишку
Існує декілька точних формул для залишкового члена Rk многочлена Тейлора, найбільш загальна з яких наступна.
Залишок у формі середнього значення. Нехай функція f : R → R — k+1 раз диференційовна на інтервалі та неперервна на відрізку . Тоді
Це залишковий член у формі Лагранжа[2]. За тих же умов
Це залишковий член у формі Коші[3].
Ці уточнення теореми Тейлора зазвичай виводяться за допомогою формули про скінченні прирости.
Можна також знайти й інші вирази для залишку. Наприклад, якщо G(t) є неперервною на закритому інтервалі та диференційовною з похідною, що не прагне до нуля на відкритому інтервалі між a і x, то
для деякого числа ξ між a і x. Ця версія охоплює форми Лагранжа та Коші як окремі випадки, і виводиться за допомогою теореми Коші про среднє значення (розширеної версії теореми Лагранжа про среднє значення).
Запис формули для залишку в інтегральної формі є більш загальним, ніж попередні формули, і вимагає розуміння інтегральної теорії Лебега. Однак вона зберігається також для інтегралу Рімана за умови, що похідна порядку (k+1) від f є неперервною на закритому інтервалі [a,x].
Інтегральна форма[4] запису формули для залишку Нехай f(k) — абсолютно неперервна на закритому інтервалі між a і x. Тоді
Внаслідок абсолютної неперервності f(k) на закритому інтервалі між a і x, її похідна f(k+1) існує як L1-функція, і цей наслідок може бути отриманий за допомогою формальних обчислень з використанням теореми Ньютона — Лейбніца та інтегрування частинами.
Оцінки залишку
На практиці часто буває корисно чисельно оцінити величину залишкового члена наближення Тейлора.
Будемо вважати, що f — (k+1)-раз неперервно диференційовна на інтервалі I, що містить a. Будемо вважати, що існує дійсні постійні числа q і Q такі, що
на всьому протязі I. Тоді залишковий член задовольняє нерівності[5]
якщо x > a, і подібна оцінка, якщо x < a. Це простий наслідок з формули залишку в формі Лагранжа. Зокрема, якщо
на інтервалі I = (a−r,a+r) з деяким r>0, то
для всіх x∈(a−r,a+r). Друга нерівність називається рівномірною оцінкою, тому що вона зберігає рівномірність для всіх x на інтервалі (a−r,a+r).
Приклад
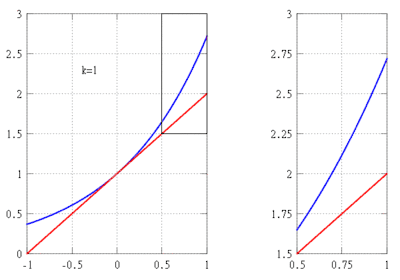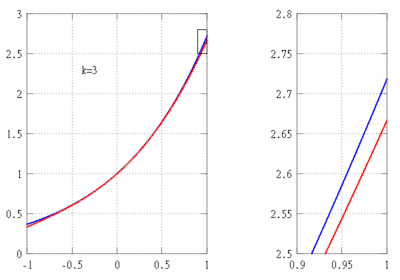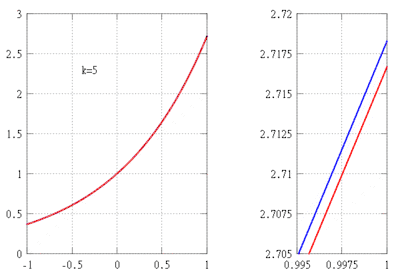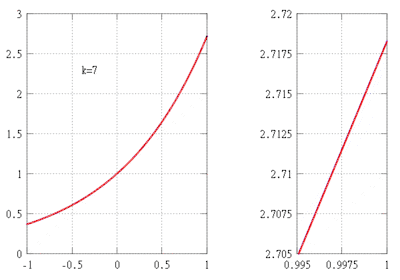
Припустимо, ми хочемо знайти наближення функції f(x) = ex на інтервалі [−1,1] й переконатися, що помилка не перевищує значення 10−5. У цьому прикладі вважаємо, що нам відомі такі властивості експоненційної функції:
З цих властивостей випливає, що f(k)(x) = ex для всіх k, і зокрема, f(k)(0) = 1. Звідси випливає, що многочлен Тейлора k-го порядку функції f в точці 0 та його залишковий член у формі Лагранжа записується за допомогою формули
де ξ — це деяке число між 0 і x. Оскільки ex зростає згідно (*), ми можемо використовувати ex ≤ 1 для x ∈ [−1, 0], щоб оцінити залишок на підінтервалі [−1, 0]. Для знаходження верхньої межі значення залишку на інтервалі [0,1], можемо використовувати властивість eξ<<ex для 0<ξ<x, щоб оцінити
використовуючи многочлен Тейлора другого порядку. Висловлюючи з цієї нерівності ex, приходимо до висновку, що
прийнявши, що чисельник приймає максимальне з усіх своїх можливих значень, а знаменник приймає мінімальне з усіх своїх можливих значень. Використовуючи ці оцінки значень ex, ми бачимо, що
і необхідна точність досягається в тому випадку, коли
(де факторіал 7!=5 040 и 8!=40 320.) Зрештою, теорема Тейлора призводить до наближення
Відзначимо, що це наближення дозволяє обчислити значення e≈2.71828 з точністю до п'ятого знака після коми.
Аналітичність
Розкладання Тейлора для дійсних аналітичних функцій
Нехай I⊂R — відкритий інтервал. За означенням, функція f:I→R — дійсна аналітична, якщо вона на даній ділянці визначена збіжністю степеневого ряду. Це означає, що для кожного a ∈ I існує деяке r > 0 і послідовність коефіцієнтів ck ∈ R така, що (a − r, a + r) ⊂ I і
Загалом, радіус збіжності степеневого ряду може бути обчислено за формулою Коші–Адамара
Цей результат базується на порівнянні з нескінченно спадною геометричною прогресією, і той же самий метод показує, що якщо степеневий ряд, розкладений по a, збігається для деякого b∈R, він повинен збігатися рівномірно на закритому інтервалі [a − rb, a + rb], де rb = |b − a|. Тут ми тільки розглянули збіжність степеневого ряду, і не виключено, що область (a − R,a + R) розширюється за межі області визначення I функції f.
Многочлен Тейлора від дійсної аналітичної функції f в точці a
це просте усіканням визначеного на деякому інтервалі відповідного степеневого ряду цієї функції, і залишковий член на даному інтервалі подається як аналітична функція
Тут функція
також є аналітичною, оскільки її степеневий ряд має той же радіус збіжності, що й вихідний ряд. За умови, що [a − r, a + r] ⊂ I і r < R, всі ці ряди збігаються рівномірно на інтервалі (a − r, a + r). Авжеж, у випадку аналітичних функцій можна оцінити залишковий член Rk(x) шляхом «обрізання» послідовності похідних f′(a) у центрі наближення, але при використанні комплексного аналізу з'являються й інші можливості, які описані нижче.
Теорема Тейлора та збіжність ряду Тейлора
Існує розбіжність між многочленами Тейлора диференційовних функцій і рядами Тейлора аналітичних функцій. Можна розглядати (справедливо) ряд Тейлора
нескінченну кількість разів диференційовної функції f:R→R як її «многочлен Тейлора нескінченно великого порядку» в точці a. Тепер оцінка залишку многочлена Тейлора має на увазі, що для будь-якого порядку k й для будь-якого r>0 існує постійна Mk,r>0 така, що
для кожного x∈(a-r, a+r). Іноді ці постійні можуть бути обрані таким чином, що Mk,r → 0, коли k → ∞ і r залишається незмінною. Тоді ряд Тейлора функції f збігається рівномірно до деякої аналітичної функції
Тут необхідно згадати важливий момент. Можлива ситуація, коли нескінченну кількість разів диференційовна функція f має ряд Тейлора в точці a, який збігається в деякому околі точки a, але гранична функція Tf відрізняється від f. Важливим прикладом цього феномену є такий
Використовуючи ланцюгове правило можна показати індуктивно, що для будь-якого порядку k,
для деякого многочлену pk. Функція прагне до нуля швидше, ніж будь-який поліном, відповідно до того, як x → 0, тоді f є нескінченну кількість разів диференційовною й f(k)(0) = 0 для кожного додатного цілого k. Тепер оцінки для залишку многочлена Тейлора функції f показують, що ряд Тейлора збігається рівномірно до нульової функції на всій дійсній числовій осі. Не буде помилки в наступних твердженнях:
- Ряд Тейлора функції f збігається рівномірно до нульової функції Tf(x)=0.
- Нульова функція є аналітичною, і кожний коефіцієнт її ряду Тейлора дорівнює нулю.
- Функція f є нескінченну кількість разів диференційовною, але не аналітичною.
- Для будь-якого k∈N и r>0 існує Mk, r>0 таке, що залишковий член многочлена Тейлора k-го порядку функції f задовільняє умові (*).
Теорема Тейлора в комплексному аналізі
Теорема Тейлора узагальнює функції , які є комплексно диференційовними на відкритій підмножині U ⊂ C комплексної площини. Однак її корисність знижена іншими теоремами комплексного аналізу, а саме: більш повні версії подібних результатів можуть бути виведені для комплексно диференційовних функцій f : U → C з використанням інтегральної формули Коші як показано нижче.
Нехай r > 0 таке, що замкнене коло B(z, r) ∪ S(z, r) міститься в U. Тоді інтегральна формула Коші з додатною параметризацією γ(t)=reit околу S(z, r) с t ∈ [0,2π] дає
Тут всі підінтегральні вирази є неперервними на околі S(z, r), що обґрунтовує диференціювання під знаком інтеграла. Зокрема, якщо f — один раз комплексно диференційовна на відкритій множині U, то вона фактично нескінченну кількість разів комплексно диференційовна на U. Маємо оцінку Коші[6]
для будь-якого z ∈ U и r > 0 таку, що B(z, r) ∪ S(c, r) ⊂ U. Ці оцінки означають, що комплексний ряд Тейлора
функції f збігається рівномірно в будь-якому колі B(c, r) ⊂ U з S(c, r) ⊂ U в деякій функції Tf. Крім того, використовуючи формулу інтегрування по контуру для похідних f(k)(c),
таким чином, будь-яка комплексно диференційовна функція f на відкритій множині U ⊂ C є комплексно аналітичною. Все те, що було написано вище для дійсних аналітичних функцій справедливо також й для комплексних аналітичних функцій, де відкритий інтервал I змінено на відкриту підмножину U ∈ C 1 a — центровані інтервали (a − r, a + r) змінено на c — центровані кола B(c, r). Зокрема, розкладання Тейлора зберігається у вигляді
де залишковий член Rk — комплексно аналітичний. При розгляданні рядів Тейлора методи комплексного аналізу дозволяють отримати кілька більш потужних результатів. Наприклад, використовуючи інтегральну формулу для будь-якої додатно орієнтованої жорданової кривої γ, яка параметризує границю ∂W ⊂ U області W ⊂ U, можна отримати вираз для похідних f(j)(c) як показано вище, і злегка змінивши розрахунки для Tf(z) = f(z), прийти до точної формули
Важлива особливість тут в тому, що якість наближення за допомогою многочлена Тейлора в області W ⊂ U є мажоріруємим значенням функції f на границі ∂W ⊂ U. Також, застосовуючи оцінки Коші до виразу залишку ряду, отримуємо рівномірні оцінки
Приклад
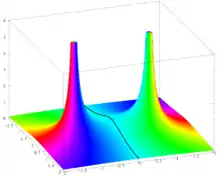
Функція f:R→R, що визначається рівнянням
дійсна аналітична, тобто в даній області визначається своїм рядом Тейлора. Один з малюнків, наведених вище, показує, що деякі функції, що задаються дуже просто, не можуть бути виражені за допомогою наближення Тейлора в околі центру наближення, якщо цей окіл занадто великий. Цю властивість легко зрозуміти в рамках комплексного аналізу. Більш конкретно, функція f розширюється до мероморфної функції
на компактифіцированій комплексній площині. Вона має прості осі в точках z=i и z=−i, і вона всюди аналітична. ЇЇ ряд Тейлора, що має центр в z0, збігається на будь-якому колі B(z0,r) с r<|z-z0|, де той же ряд Тейлора збігається при z∈C. Внаслідок цього ряд Тейлора функції f, що має центр в точці 0, збігається на B(0,1) і він не збігається для будь-якого z∈C с |z|>1 внаслідок наявних осей в точках i и −i. За тих же причин ряд Тейлора функції f, що має центр в точці 1, збігається на B(1,√2) і не збігається для будь-якого z∈C с |z-1|>√2.
Узагальнення теореми Тейлора
Вищі порядки диференційовності
Функція f:Rn → R — диференційовна в точці a ∈ Rn тоді й тільки тоді, коли існує лінійна форма L : Rn → R і функція h : Rn → R така, що
Якщо цей випадок має місце, то L = df(a) є диференціал функції f в точці a. Крім того, коли частинні похідні функції f існують в точці a, то диференціал f в точці a визначено формулою
Вводячи мультиіндекс, запишемо
для α ∈ Nn і x ∈ Rn. Якщо всі частинні похідні k-го порядку функції f : Rn → R — неперервні в a ∈ Rn, то згідно з теоремою Клеро, можна змінити порядок змішаних похідних в точці a, тоді запис
для частинних похідних вищих порядків є правомірним у цій ситуації. Теж саме є правильним, якщо всі частинні похідні (k − 1)-го порядку функції f існують в деякому околі точки a і диференційовні в точці a. Тоді можна сказати, що функція f — k разів диференційовна в точці a .
Теорема Тейлора для функцій багатьох змінних
Теорема Тейлора для функцій багатьох змінних. Нехай f : Rn → R — k разів диференційовна функція в точці a∈Rn. Тоді існує hα : Rn→R така, що
Якщо функція f : Rn → R — k+1 разів неперервно диференційовна в замкненій кулі B, то можна отримати точну формулу для залишку розкладання Тейлора до частинних похідних (k+1)-го порядку від f в цьому околі. А саме
У цьому випадку, внаслідок неперервності частинних похідних (k+1)-го порядку на компактній множині B, безпосередньо отримуємо
Докази
Доказ теореми Тейлора для однієї дійсної змінної
Нехай[7]
де, як вказано в формулюванні теореми Тейлора,
Достатньо показати, що
Доказ засновано на повторюваному застосуванні правила Лопіталя. Помітимо, що кожне j = 0,1,…,k−1, . Звідси кожна наступна похідна чисельника функції прагне до нуля в точці , і теж саме справедливо для знаменника. Тоді
де перехід від передостаннього виразу до останнього випливає з визначення похідної в точці x = a.
Примітки
- Hazewinkel, Michiel, ред. (2001). t/t092300. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.
- Klein, 1998, §20.3; Apostol, 1967, §7.7.
- Apostol, 1967, §7.7.
- Apostol, 1967, §7.5.
- Apostol, 1967, §7.6
- Rudin, 1987, § 10.26.
- Stromberg, 1981
Джерела
- Apostol, Tom (1967). Calculus. Jon Wiley & Sons, Inc. ISBN 0-471-00005-1..
- Bartle; Sherbert (2000). Introduction to Real Analysis (вид. 3rd). John Wiley & Sons, Inc. ISBN 0-471-32148-6..
- Hörmander, L. (1976). Linear Partial Differential Operators, Volume 1. Springer-Verlag. ISBN 978-3540006626..
- Klein, Morris (1998). Calculus: An Intuitive and Physical Approach. Dover. ISBN 0-486-40453-6..
- Pedrick, George (1994). A First Course in Analysis. Springer-Verlag. ISBN 0-387-94108-8..
- Stromberg, Karl (1981). Introduction to classical real analysis. Wadsworth, Inc. ISBN 978-0534980122..
- Rudin, Walter (1987). Real and complex analysis, 3rd ed. McGraw-Hill Book Company. ISBN 0-07-054234-1..
Посилання
- Формула Тейлора // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 277. — 594 с.
- Taylor Series Approximation to Cosine
- Trigonometric Taylor Expansion interactive demonstrative applet
- Taylor Series Revisited at Holistic Numerical Methods Institute
