Числення багатьох змінних
Числення багатьох змінних або аналіз функцій багатьох змінних — це область математичного аналізу, що є продовженням теорії обчислення із однією змінною до випадку обчислення функцій із багатьма змінними: диференціювання і інтегрування функцій, що мають багато змінних, а не одну.[1]
| Розділи в | ||||||
| Математичному аналізі | ||||||
|---|---|---|---|---|---|---|
|
||||||
|
||||||
|
||||||
|
||||||
|
Спеціалізовані |
||||||
Застосування
Методи аналізу функцій багатьох зміних використовуються для вивчення різних об’єктів і явищ матеріального світу. Зокрема,
| Область визначення і відображення | Методи | ||
|---|---|---|---|
| Криві | 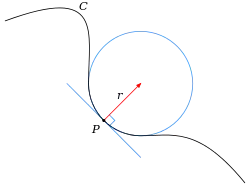 | Довжини кривих, лінійні інтеграли, і кривина. | |
| Поверхні |  | Площі поверхонь, поверхневі інтеграли, густина потоку енергії через поверхню, і опуклість. | |
| Скалярне поле | 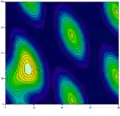 | Максимуми і мінімуми, Метод невизначених множників, Похідна за напрямком, рівневі поверхні. | |
| Векторне поле |  | будь-які операції з векторного числення включаючи градієнт, дивергенцію, і ротор. |
Числення багатьох змінних можна застосувати для аналізу детермінованих систем, що мають багато ступенів свободи. Функції із незалежними змінними, що відповідають кожному із ступенів свободи часто використовують для моделювання цих систем, а числення багатьох змінних надає інструментарій для характеристики динаміки системи.
Числення багатьох змінних використовується в теорії оптимального управління динамічними системами неперервного часу. І застосовується в регресійному аналізі для отримання формул, що визначають зв'язок між різноманітними наборами емпіричних даних.
Не детерміновані, або стохастичні системи вивчають за допомогою інших видів математики, таких як теорія випадкових процесів.
Границі і неперервність
Вивчення границь і неперервності в аналізі функцій багатьох змінних приводить до багатьох не інтуїтивних результатів, які не можна продемонструвати з функціями однієї змінної.[1] Наприклад, існують скалярні функції двох змінних, що мають такі точки в їх області функцій, які мають певну границю при наближенні до будь-якої довільної прямої і мають іншу границю при наближенні здовж параболи.

Насправді, функція
наближується до нуля здовж будь-якої прямої, що проходить через початок координат. Однак, коли початок наближується здовж параболи , вона має границю . Оскільки вибір різних шляхів до однієї і тієї ж точки приводить до різних значень границі, границя не існує.
Безперервність функції для кожного аргументу не є достатньою для багатозмінної безперервності.[1] Наприклад, у випадку функції дійсних чисел із двома параметрами, , неперервність функції для при фіксованому значенні і неперервність для при фіксованому значенні не означає неперервність функції .
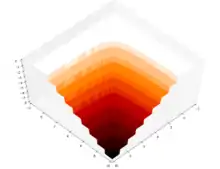
Розглянемо
Легко пересвідчитися, що всі функції дійсних значень (із одним дійсним аргументом) що задані є неперервними по відношенню до (для будь-яких фіксованих значень ). Відповідно, всі є неперервними оскільки є симетричною відносно і . Однак, сама не є неперервною, це можна побачити розглянувши послідовність (для натурального числа ), що мала б збігатися до якби була неперервною. Однак, Таким чином функція не є неперервною в .
Часткова похідна
Поняття часткової похідної узагальнює поняття похідної для вищих порядків. Часткова похідна функції багатьох змінних є похідною однієї змінної при умові, що всі інші змінні залишаються сталими.[1]
Часткові похідні можна поєднати цікавими способами, аби утворити більш складні вирази похідної. У векторному численні, оператор набла () використовують для визначення понять градієнта, дивергенції, і ротора в термінах часткових похідних. Для представлення похідної функції між двома просторами довільної розмірності можна використати матрицю часткових похідних, що називається матрицею Якобіана. Похідні таким чином можна зрозуміти як лінійне відображення, яке безпосередньо змінюється від точки до точки в області функції.
Диференціальні рівняння, що містять часткові похідні називаються диференціальними рівняннями з частковими похідними. Ці рівняння зазвичай набагато важче розв'язувати ніж звичайні диференціальні рівняння, що містять похідні лише однієї змінної.[1]
Багатократний інтеграл
Багатократний інтеграл розширює поняття інтеграла до функції з будь-якою кількістю змінних. Подвійні чи потрійні інтеграли можуть використовуватися для визначення площ чи об'ємів областей на площині і в просторі. Теорема Фубіні гарантує, що багатократний інтеграл може розраховуватися як повторний інтеграл при умові що функція яка інтегрується не безперервною по всій області інтегрування.[1]
Поверхневий інтеграл і криволінійний інтеграл використовуються для інтегрування по викривленим многовидам, наприклад, по поверхням і кривим.
Див. також
Примітки
- Richard Courant; Fritz John (14 грудня 1999). Introduction to Calculus and Analysis Volume II/2. Springer Science & Business Media. ISBN 978-3-540-66570-0.
Посилання
- Диференціальне числення функції багатьох змінних // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 345. — 594 с.
- UC Berkeley video lectures on Multivariable Calculus, Fall 2009, Professor Edward Frenkel
- MIT video lectures on Multivariable Calculus, Fall 2007
- Multivariable Calculus: A free online textbook by George Cain and James Herod
- Multivariable Calculus Online: A free online textbook by Jeff Knisley
- Multivariable Calculus – A Very Quick Review Архівовано 24 березня 2012 у Wayback Machine., Prof Blair Perot, University of Massachusetts Amherst
